Relative Velocity
Problems from IIT JEE
Problem (IIT JEE 1988): A boat, which has a speed of 5 km/hr in still water, crosses a river of width 1 km along the shortest possible path is 15 minutes. The velocity of the river water (in km/hr) is,
- $1$
- $3$
- $4$
- $\sqrt{41}$
Solution:
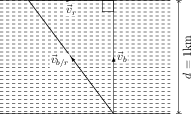 The boat crosses the river by the shortest path if it moves perpendicular to the river current (see figure). Let $\vec{v}_{b}$ and $\vec{v}_{r}$ be the velocities of the boat and the river current w.r.t. the ground. The velocity of the boat in still water is equal to the relative velocity of the boat w.r.t. water i.e.,
\begin{align}
\vec{v}_{b/r}=\vec{v}_b-\vec{v}_r,
\end{align}
which gives,
\begin{align}
\label{ctb:eqn:2}
|\vec{v}_{b/r}|^2=|\vec{v}_b|^2+|\vec{v}_r|^2.\qquad (\because \vec{v}_b\perp\vec{v}_r).
\end{align}
Given, speed of the boat in still water $|\vec{v}_{b/r}|={5}\;\mathrm{km/hr}$ and the speed of the boat relative to the ground,
\begin{align}
|\vec{v}_b|=\frac{d}{t}=\frac{1}{15/60}={4}\;\mathrm{km/hr}.
\end{align}
Substitute $|\vec{v}_b|$ and $|\vec{v}_{b/r}|$ to get $|\vec{v}_r|={3}\;\mathrm{km/hr}$.
The boat crosses the river by the shortest path if it moves perpendicular to the river current (see figure). Let $\vec{v}_{b}$ and $\vec{v}_{r}$ be the velocities of the boat and the river current w.r.t. the ground. The velocity of the boat in still water is equal to the relative velocity of the boat w.r.t. water i.e.,
\begin{align}
\vec{v}_{b/r}=\vec{v}_b-\vec{v}_r,
\end{align}
which gives,
\begin{align}
\label{ctb:eqn:2}
|\vec{v}_{b/r}|^2=|\vec{v}_b|^2+|\vec{v}_r|^2.\qquad (\because \vec{v}_b\perp\vec{v}_r).
\end{align}
Given, speed of the boat in still water $|\vec{v}_{b/r}|={5}\;\mathrm{km/hr}$ and the speed of the boat relative to the ground,
\begin{align}
|\vec{v}_b|=\frac{d}{t}=\frac{1}{15/60}={4}\;\mathrm{km/hr}.
\end{align}
Substitute $|\vec{v}_b|$ and $|\vec{v}_{b/r}|$ to get $|\vec{v}_r|={3}\;\mathrm{km/hr}$.
