RC, LR, and LC Circuits with DC and AC Sources

Problems from IIT JEE

Problem (IIT JEE 2001): An inductor of inductance $L={400}\;\mathrm{mH}$ and resistors of resistance $R_1={2}\;\mathrm{\Omega}$ and $R_2={2}\;{\Omega}$ are connected to a battery of emf $E={12}\;\mathrm{V}$ as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time $t=0$. What is the potential drop across $L$ as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through $R_1$ as a function of time?

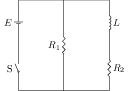
Solution: Let $i$ be the current through the inductor $L$ and the resistor $R_2$ (see figure). The potential drop across $L$ is $L\frac{\mathrm{d}i}{\mathrm{d}t}$ and potential drop across $R_2$ is $iR_2$. Kirchhoff's loop law gives,

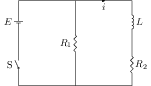
\begin{alignat}{2} &L\frac{\mathrm{d}i}{\mathrm{d}t}+iR_2-E=0. \end{alignat} Integrate above equation and use initial condition $i=0$ at $t=0$ to get, \begin{alignat}{2} &i=\frac{E}{R_2}\left[1-e^{-tR_2/L}\right]. \nonumber \end{alignat} The potential drop across $L$ is given by, \begin{align} V_L &=L\frac{\mathrm{d}i}{\mathrm{d}t} \\ &=Ee^{-tR_2/L} \\ &=12e^{-t\times 2/0.4} \\ &=12e^{-5t}. \nonumber \end{align} In the steady state ($t\to\infty$), the current through $L$ is $i_0={E}/{R_2}={6}\;\mathrm{A}$, $V_L=0$, and $V_{R_2}={12}\;\mathrm{V}$.

Let $i$ be the decaying current in the circuit when switch is opened (see figure). The potential across $L$ is $L\frac{\mathrm{d}i}{\mathrm{d}t}$, potential across $R_1$ is $iR_1$, and that across $R_2$ is $iR_2$. Kirchhoff's loop law gives,

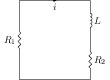
\begin{alignat}{2} &L\frac{\mathrm{d}i}{\mathrm{d}t}+iR_1+iR_2=0. \end{alignat} Integrate above equation with initial condition $i=i_0={6}\;\mathrm{A}$ at $t=0$ to get, \begin{alignat}{2} & i=i_0e^{-t(R_1+R_2)/L}. \end{alignat} Substitute $R_1={2}\;\mathrm{\Omega}$, $R_2={2}\;\mathrm{\Omega}$ and $L={0.4}\;\mathrm{H}$ in above equation to get current through $R_1$ as a function of time $t$, \begin{align} i&=i_0 e^{-t(R_1+R_2)/L} \\ &=6e^{-t (2+2)/0.4}\\ &=6e^{-10t}. \nonumber \end{align}