Kinematics in One and Two Dimensions
Motion in Straight Line with Constant Acceleration
Let a particle be moving with a constant acceleration $a$. Let the velocity at time $t=0$ be $u$. The distance $s$ travelled by the particle in time $t$ and its velocity at time $t$ are relate to $u$ and $a$ by \begin{align} & v=u+at \\ & s=ut+\tfrac{1}{2}at^2\\ & v^2-u^2=2as. \end{align}Problems from IIT JEE
Problem (IIT JEE 2014):
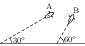 Airplanes A and B are flying with constant velocity in the same vertical plane at angles $30^\mathrm{o}$ and $60^\mathrm{o}$ with respect to the horizontal respectively as shown in figure. The speed of A is $100\sqrt{3}\;\mathrm{m/s}$. At time $t={0}\;\mathrm{s}$, an observer in A finds B at a distance of 500 m. This observer sees B moving with a constant velocity perpendicular to the line of motion of A. If at $t=t_0$, A just escapes being hit by B, $t_0$ in seconds is,
Airplanes A and B are flying with constant velocity in the same vertical plane at angles $30^\mathrm{o}$ and $60^\mathrm{o}$ with respect to the horizontal respectively as shown in figure. The speed of A is $100\sqrt{3}\;\mathrm{m/s}$. At time $t={0}\;\mathrm{s}$, an observer in A finds B at a distance of 500 m. This observer sees B moving with a constant velocity perpendicular to the line of motion of A. If at $t=t_0$, A just escapes being hit by B, $t_0$ in seconds is,
Solution:
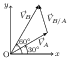 Let $\vec{V}_\text{A}$ and $\vec{V}_\text{B}$ be the velocity vectors of airplane A and B in a frame attached to the ground. The figure shows $\vec{V}_\text{A}$, $\vec{V}_\text{B}$, and $\vec{V}_\text{B/A}$, the velocity of B relative to A. The expressions for these three vectors are,
\begin{alignat}{2}
\label{fxb:eqn:1}
&\vec{V}_\text{A}=100\sqrt{3}\cos30\,\hat{\imath}+100\sqrt{3} \sin30\,\hat{\jmath}=150\,\hat{\imath}+50\sqrt{3}\,\hat{\jmath}, \\
\label{fxb:eqn:2}
&\vec{V}_\text{B}=V_\text{B}\cos60\,\hat\imath+V_\text{B}\sin60\,\hat\jmath=\frac{V_\text{B}}{2}\,\hat\imath+\frac{\sqrt{3}V_\text{B}}{2}\,\hat\jmath, \\
\label{fxb:eqn:3}
& \vec{V}_\text{B/A}=\vec{V}_\text{B}-\vec{V}_\text{A}=\left(\frac{V_\text{B}}{2}-150\right)\hat\imath+\sqrt{3}\left(\frac{V_\text{B}}{2}-50\right)\hat\jmath.
\end{alignat}
The observer in A sees B moving with a constant velocity perpendicular to the line of motion of A i.e., $\vec{V}_\text{B/A}\perp \vec{V}_\text{A}$. Thus,
\begin{alignat}{2}
\label{fxb:eqn:4}
&\vec{V}_\text{B/A}\cdot\vec{V}_\text{A}=150(V_\text{B}-200)=0.
\end{alignat}
Solve above equation to get $V_\text{B}={200}\;\mathrm{m/s}$. Substitute $V_\text{B}$ to get $\vec{V}_\text{B/A}=-50\hat\imath+50\sqrt{3}\hat\jmath$ and $|\vec{V}_\text{B/A}|={100}\;\mathrm{m/s}$. The time taken to travel a relative distance of 500 m with a relative speed of 100 m/s is $t_0=500/100={5}\;\mathrm{s}$.
Let $\vec{V}_\text{A}$ and $\vec{V}_\text{B}$ be the velocity vectors of airplane A and B in a frame attached to the ground. The figure shows $\vec{V}_\text{A}$, $\vec{V}_\text{B}$, and $\vec{V}_\text{B/A}$, the velocity of B relative to A. The expressions for these three vectors are,
\begin{alignat}{2}
\label{fxb:eqn:1}
&\vec{V}_\text{A}=100\sqrt{3}\cos30\,\hat{\imath}+100\sqrt{3} \sin30\,\hat{\jmath}=150\,\hat{\imath}+50\sqrt{3}\,\hat{\jmath}, \\
\label{fxb:eqn:2}
&\vec{V}_\text{B}=V_\text{B}\cos60\,\hat\imath+V_\text{B}\sin60\,\hat\jmath=\frac{V_\text{B}}{2}\,\hat\imath+\frac{\sqrt{3}V_\text{B}}{2}\,\hat\jmath, \\
\label{fxb:eqn:3}
& \vec{V}_\text{B/A}=\vec{V}_\text{B}-\vec{V}_\text{A}=\left(\frac{V_\text{B}}{2}-150\right)\hat\imath+\sqrt{3}\left(\frac{V_\text{B}}{2}-50\right)\hat\jmath.
\end{alignat}
The observer in A sees B moving with a constant velocity perpendicular to the line of motion of A i.e., $\vec{V}_\text{B/A}\perp \vec{V}_\text{A}$. Thus,
\begin{alignat}{2}
\label{fxb:eqn:4}
&\vec{V}_\text{B/A}\cdot\vec{V}_\text{A}=150(V_\text{B}-200)=0.
\end{alignat}
Solve above equation to get $V_\text{B}={200}\;\mathrm{m/s}$. Substitute $V_\text{B}$ to get $\vec{V}_\text{B/A}=-50\hat\imath+50\sqrt{3}\hat\jmath$ and $|\vec{V}_\text{B/A}|={100}\;\mathrm{m/s}$. The time taken to travel a relative distance of 500 m with a relative speed of 100 m/s is $t_0=500/100={5}\;\mathrm{s}$.
Problem (IIT JEE 1997): The trajectory of a projectile in a vertical plane is $y=ax-bx^2$, where $a$, $b$ are constants, and $x$ and $y$ are respectively the horizontal and vertical distances of the projectile from the point of projection. The maximum height attained is _______ and the angle of projection from the horizontal is _______.
Solution: Trajectory equation is $y=ax-bx^2$. The slope of the trajectory is zero at maximum height i.e., \begin{alignat}{2} \label{otb:eqn:1} &\frac{\mathrm{d}y}{\mathrm{d}x}=a-2bx=0. \end{alignat} Solve above equtaion to get $x={a}/{(2b)}$. Substitute it in the given trajectory equation to get the maximum height, \begin{align} y_\text{max}=a\left(\frac{a}{2b}\right)-b\left(\frac{a}{2b}\right)^2=\frac{a^2}{4b}. \end{align} The slope of trajectory at the projection point is given by, \begin{align} \tan\theta=\frac{\mathrm{d}y}{\mathrm{d}x}\Big|_{x=0}=a-2b(0)=a. \end{align} Thus, the angle of projection is $\theta=\tan^{-1}a$.
Problem (IIT JEE 1993): A small block slides without friction down an inclined plane starting from rest. Let $s_n$ be the distance travelled from $t=n-1$ to $t=n$. Then $\frac{s_n}{s_{n+1}}$ is,
- $\frac{2n-1}{2n}$
- $\frac{2n+1}{2n-1}$
- $\frac{2n-1}{2n+1}$
- $\frac{2n}{2n+1}$
Solution: The downward acceleration of the block on an inclined plane with inclination angle $\theta$ is given by $a=g\sin\theta$. Initial velocity of the block is $u=0$. The distance travelled in the first $n$ seconds is given by, \begin{alignat}{2} &s(n)=u n+\tfrac{1}{2}g\sin\theta\, n^2=\tfrac{1}{2}\,g\sin\theta \,n^2. \nonumber \end{alignat} Thus, the distances travelled in the $n^\mathrm{th}$ and the $(n+1)^\mathrm{th}$ seconds are, \begin{align} \label{htb:eqn:1} &s_n=s(n)-s(n-1)=(2n-1)\, \tfrac{1}{2}\,g\sin\theta, \\ \label{htb:eqn:2} &s_{n+1}=s(n+1)-s(n)=(2n+1)\, \tfrac{1}{2}\,g\sin\theta. \end{align} Divide first equation by the second equation to get $\frac{s_n}{s_{n+1}}=\frac{2n-1}{2n+1}$.
