Electric Field Lines
An electrostatic field line originate at a positive charge and terminate at a negative charge. No two lines intersect with each other. The density of field lines indicates the magnitude of the electric field. If density is more then field strength is high.
Problems from IIT JEE
Problem (IIT JEE 2010): A few electric field lines for a system of two charges $Q_1$ and $Q_2$ fixed at two different points on the $x$-axis are shown in the figure. These lines suggest that,
- $|Q_1|>|Q_2|$.
- $|Q_1|<|Q_2|$.
- at a finite distance to the left of $Q_1$ the electric field is zero.
- at a finite distance to the right of $Q_2$ the electric field is zero.
Solution: From the direction of electric field lines, $Q_1$ is positive and $Q_2$ is negative. The density of electric field lines (which is an indication of flux) is more around $Q_1$ in comparison to that around $Q_2$. In other words, flux $\phi_1$ through a small sphere containing $Q_1$ is more than flux $ \phi_2$ through a similar sphere containing $Q_2$. From Gauss's law, flux $\phi=q_\text{enc}/\epsilon_0$. Thus, $\phi_1>\phi_2$ implies $|Q_1|>|Q_2|$. The electric field at a distance $x$ towards right of $Q_2$ is given by \begin{align} |\vec{E}|&=\frac{1}{4\pi\epsilon_0}\frac{Q_1}{(d+x)^2}-\frac{1}{4\pi\epsilon_0}\frac{Q_2}{x^2},\nonumber \end{align} where $d$ is separation between $Q_1$ and $Q_2$. Since $Q_1>Q_2$, the $|\vec{E}|$ becomes zero for some finite $x$. The readers are encouraged to show that there are two such points given by \begin{align} x_1&=\frac{Q_2+\sqrt{Q_1Q_2}}{Q_1-Q_2}d, \nonumber\\ x_2&=\frac{Q_2-\sqrt{Q_1Q_2}}{Q_1-Q_2}d.\nonumber \end{align} Also, show that the electric field is non-zero at all finite distances towards left of $Q_1$. Draw the electric field lines in entire region. Thus, correct options are A and D.
Problem: Two charges $+q_1$ and $-q_2$ are placed at A and B respectively. A line of force emerges from $q_1$ at an angle $\alpha$ with line AB. At what angle will it terminate at $-q_2$?
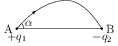
Solution: Consider an ice-cream cone of half angle $\alpha$, slant distance $r$ ($r\ll\mathrm{AB}$) and vertex at A (see figure). It can be shown that area of its spherical curved surface is $2\pi r^2(1-\cos\alpha)$. Since $r\ll \mathrm{AB}$, we can assume that field on the spherical shell of radius $r$ centred at A is $\vec{E}=\frac{q_1\,\hat{r}}{4\pi\epsilon_0 r^2} $. Thus, flux going out through the spherical curved surface of the cone is $\phi_1=\int \vec{E}\cdot\mathrm{d}\vec{S}=\frac{q_1(1-\cos\alpha)}{2\epsilon_0}$.
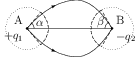
Let this line of force makes an angle $\beta$ at B. Consider an ice-cream cone of half angle $\beta$, slant distance $r$ and vertex at B. The area of its spherical curved surface is $2\pi r^2(1-\cos\beta)$ and flux going into the spherical curved surface is $\phi_2=\int \vec{E}\cdot\mathrm{d}\vec{S}=\frac{q_2(1-\cos\beta)}{2\epsilon_0}$.
Now, note that line of forces do not intersect with each other. Thus, number of lines of forces emanating from $q_1$ into the cone of half angle $\alpha$ is equal to the number of lines of forces terminating at $-q_2$ into the cone of half angle $\beta$. Since number of lines of forces indicates flux, we conclude that $\phi_1=\phi_2$. Solve to get \begin{align} \beta=\cos^{-1}\left(1-\frac{q_1}{q_2}(1-\cos\alpha)\right).\nonumber \end{align}
