Gauss's Law and its Applications

By Jitender Singh on Dec 9, 2022

By Gauss's law, the flux of electric field $\vec{E}$ through a closed surface $S$ is equal to the algebraic sum of the charges enclosed by this surface, divided by $\epsilon_0$ i.e., \begin{align} \oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{q_{enc}}{\epsilon_0} \end{align}

Field due to line charge

Consider an infinitely long line charge having uniform linear charge density $\lambda$. The electric field at a distance $r$ from it is given by \begin{align} E=\frac{\lambda}{2\pi\epsilon_0 r}. \end{align}

Field due infinite plane sheet

The electric field of an infinite plane sheet having uniform charge density $\sigma$ is given by \begin{align} E=\frac{\sigma}{2\epsilon_0}. \end{align}

Electric Field due to Uniformly Charged Thin Spherical Shell

Consider a thin spherical shell of radius $R$. A charge $Q$ is uniformly distributed over its surface.

The electric field due to this shell is given by \begin{align} E&=\left\{\begin{array}{ll} 0, & \text{for } r < R \\ \frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}, & \text{for } r\geq R \end{array}\right. \end{align}

The electric potential by the shell is given by \begin{align} V=\left\{\begin{array}{ll} \frac{1}{4\pi\epsilon_0}\frac{Q}{R}, & \text{for } r < R\\ \frac{1}{4\pi\epsilon_0}\frac{Q}{r}, & \text{for } r\geq R \end{array}\right. \end{align}

electric-potential-due-to-spherical-shell

Problems from IIT JEE

Problem (IIT JEE 2015): An infinitely long uniform charge distribution of charge per unit length $\lambda$ lies parallel to the $y$-axis in the $y\text{-}z$ plane at $z=\frac{\sqrt{3}}{2}a$ (see figure). If the magnitude of the flux of the electric field through the rectangular surface ABCD lying in the $x\text{-}y$ plane with its centre at the origin is $\lambda L/(n\epsilon_0)$ ($\epsilon_0=$ permitivity of free space), then the value of $n$ is,

Solution: The situation is shown in the figure.

an-infinitely-long-uniform-charge-solution

Consider a cylindrical Gaussian surface of radius $a\sqrt{3}/2$ and length $L$. The charge enclosed by the Gaussian surface is $q_\text{enc}=\lambda L$. Apply Gauss's law to get total flux through the Gaussian surface, \begin{align} \phi &={q_\text{enc}}/{\epsilon_0} \\ &=\lambda L/\epsilon_0.\nonumber \end{align} The flux through the rectangular surface is equal to the flux through the cylindrical section with chord PQ (see figure). From geometry, the chord PQ subtends an angle $\alpha={60}\;\mathrm{deg}$ at the axis of the cylinder. Thus, the flux through the rectangular surface is, \begin{align} \phi_\text{rectangle} & =\phi\,(\alpha/360) \\ &=(\lambda L/\epsilon_0)\,(60/360) \\ &=\lambda L/(6\epsilon_0).\nonumber \end{align}

Problem (IIT JEE 2005): Three infinitely long charge sheets are placed parallel to $x\text{-}y$ plane as shown in the figure. The electric field at point P is,

$\frac{2\sigma}{\epsilon_0}\hat{k}$
$-\frac{2\sigma}{\epsilon_0}\hat{k}$
$\frac{4\sigma}{\epsilon_0}\hat{k}$
$-\frac{4\sigma}{\epsilon_0}\hat{k}$

Solution: The electric field at P is given by, \begin{align} \vec{E} & =\frac{-\sigma}{2\epsilon_0} \hat{k}+\frac{-2\sigma}{2\epsilon_0}\hat{k}+\frac{\sigma}{2\epsilon_0} (-\hat{k}) \\ &=-\frac{2\sigma}{\epsilon_0}\hat{k}.\nonumber \end{align}

Problem (IIT JEE 2015): Consider a uniform spherical charge distribution of radius $r_1$ centered at the origin O. In this distribution, a spherical cavity of radius $r_2$, centered at P with distance $\mathrm{OP}=a=r_1-r_2$ (see figure) is made. If the electric field inside the cavity at position $\vec{r}$ is $\vec{E}(\vec{r})$, then the correct statement(s) is(are),

$\vec{E}$ is uniform, its magnitude is independent of $r_2$ but its direction depends on $\vec{r}$.
$\vec{E}$ is uniform, its magnitude depends on $r_2$ and its direction depends on $\vec{r}$.
$\vec{E}$ is uniform, its magnitude is independent of $a$ but its direction depends on $\vec{a}$.
$\vec{E}$ is uniform and both its magnitude and direction depend on $\vec{a}$.

Solution:

Let $\rho$ be the charge density of the spherical charge distribution of radius $r_1$ centred at the origin O. A spherical cavity of radius $r_2$ centred at P with distance $\mathrm{OP}=a=r_1-r_2$ is made in the spherical distribution (see figure). The sphere with cavity is equivalent to a sphere of uniform charge density $-\rho$ and radius $r_2$ centred at P embedded in the original sphere. Thus, electric field at a point Q in the cavity is superposition of (i) electric field at Q due to the sphere of charge density $\rho$ and radius $r_1$ centred at O (say $\vec{E}_1$), and (ii) electric field at Q due to the sphere of charge density $-\rho$ and radius $r_2$ centred at P (say $\vec{E}_2$). Let $\vec{a}$, $\vec{r}$, and $\vec{r}-\vec{a}$ be the vectors as shown in the figure. The electric fields $\vec{E}_1$, $\vec{E}_2$, and their superposition $\vec{E}_{12}$ are given by, \begin{align} &\vec{E}_1=\frac{1}{4\pi\epsilon_0}\frac{\frac{4}{3}\pi |\vec{r}|^3\rho}{|\vec{r}|^2}\hat{r}=\frac{\rho}{3\epsilon_0}\,\vec{r},\\ &\vec{E}_2=-\frac{\rho}{3\epsilon_0}\,(\vec{r}-\vec{a}),\\ &\vec{E}_{12}=\vec{E}_1+\vec{E}_2=\frac{\rho}{3\epsilon_0}\,\vec{a}. \end{align} Thus, electric field at a point within the cavity is uniform and both its magnitude and direction depend on $\vec{a}$. The readers are encouraged to draw the electric lines of forces both inside and outside the cavity.

Some Applications of Gauss's Law

Example 1: Suppose that we have in vacuum a system of fixed point charges in equilibrium. Let us consider one of these charges, e.g. a charge $q$. Can its equilibrium be stable? The answer is no.

Example 2: The electric field of a uniformly charged plane sheet with surface charge density $\sigma$? The answer is $\vec{e}=\frac{\sigma}{2\epsilon_0}\hat{n}$.

Example 3: The electric field of two parallel planes charged uniformly with densities $\sigma$ and $-\sigma$? The field in space between two planes is $\vec{e}=\frac{\sigma}{\epsilon_0}\hat{n}$ and it is zero outside this space.

Example 4: The electric field of an infinite circular cylinder uniformly charged over the surface so that the charge $\lambda$ corresponds to its unit length? The field is given by $\vec{E}=\frac{\lambda}{2\pi\epsilon_0}\hat{r}$.

Example 5: The electric field of a spherical surface uniformly charged by the charge $q$? The field is given by $\vec{E}=\frac{q}{4\pi\epsilon_0 r^2}\hat{r}$ for points outside the sphere and $\vec{E}=\frac{q r}{4\pi\epsilon_0 a^3}\hat{r}$, where $a$ is radius of the sphere.

Problems from Concepts of Physics

Problem: (COP Volume 2 Chapter 30 Exercise 17): A nonconducting sheet of large surface area and thickness $d$ contains uniform charge distribution of density $\rho$. Find the electric field at a point $P$ inside the plate at a distance $x$ from the central plane. Draw a qualitative graph of $E$ agains $x$ for $0

Solution: (Download pdf) Since surface area of the sheet is large, we can assume this to be an infinite sheet. By symmetry, the direction of the electric field inside (as well as outside) the sheet is perpendicular to its surface and is in outward direction (if $\rho$ is positive). Also, the field at central plane should be zero.

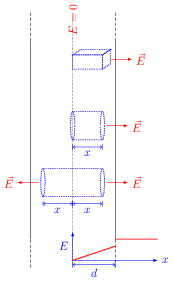
Consider a cylinder of length $x$, cross-section area $A$ ($=\pi r^2$) and one of its face located on the central plane (see middle figure) as the Gaussian surface. The flux through the curved surface of this cylinder is zero because field is perpendicular to the area element on the curved surface i.e., $\mathrm{d}\phi=\vec{E}\cdot \mathrm{d}\vec{A}=|\vec{E}| |\mathrm{d}\vec{A}|\cos90=0$. The flux through the face on the central plane is zero because $E=0$ on the central plane. The flux through the other face is $E_\text{in}A$, where $E_\text{in}$ is the field inside the plate at a distance $x$ from the central plane. Thus, total flux through this Gaussian surface is $\phi=E_\text{in} A$. The charge enclosed in this Gaussian surface is $q_{en}=\rho V= \rho A x$. Thus, by Gauss's law, $\phi=q_{en}/\epsilon$ i.e., $E_\text{in}A=\rho A x/\epsilon$ which gives $E_\text{in}=\rho x/\epsilon$ (here $\epsilon$ is the permittivity of the insulator).

For field outside the plate, consider a similar cylinder but of length $x>d$. The flux through this cylinder is $\phi=E_\text{out} A$ and charge enclosed in this is $q_\text{en}=\rho A d$. Apply Gauss's law to get $E_\text{out}=\rho d/\epsilon_0$. Note that the field outside is independent of $x$ i.e., it is a constant. Here $\epsilon_0$ is permittivity of the free space. Note that field is not continuous at $x=d$ (because $\epsilon\neq \epsilon_0$). Generally, field on the boundary of charged insulators is dis-continuous.

This problem can be solved using different Gaussian surfaces. The readers are encouraged to find the field by using other Gaussian surfaces shown in the figure.

Problem (IIT JEE 2006): For spherical symmetrical charge distribution, variation of electric potential, $V$, with distance from centre, $r$, is given in figure. Which of the following option(s) is (are) correct,

Total charge within $2R_0$ is $q$.
Total electrostatic energy for $r\leq R_0$ is zero.
At $r=R_0$ electric field is discontinuous.
There will be no charge anywhere except at $r=R_0$.

Solution: Use relation, $E=-\frac{\mathrm{d}V}{\mathrm{d}r}$, to get electric field for given potential, \begin{align} V(r)&= \begin{cases} \frac{q}{4\pi\epsilon_0 R_0} & \text{if $r\leq R_0$,} \\ \frac{q}{4\pi\epsilon_0 r} & \text{if $r>R_0$}, \\ \end{cases} \end{align} \begin{align} E(r)&= \begin{cases} 0 & \text{if $r\leq R_0$,} \\ \frac{q}{4\pi\epsilon_0 r^2} & \text{if $r>R_0$.} \\ \end{cases} \nonumber \end{align} Consider a spherical shell of radius $2R_0$ as Gaussian surface. Using Gauss's law for this surface, we get, \begin{align} q_\text{enc}&=\epsilon_0\phi \nonumber\\ &=\epsilon_0\cdot \frac{q}{16\pi\epsilon_0 R_0^2} \cdot 16\pi R_0^2 \nonumber\\ &=q.\nonumber \end{align} The electrostatic energy density for $r\leq R_0$ is $\frac{1}{2}\epsilon_0 E^2=0$ (since $E=0$) and hence total electric energy stored in this region is zero. The electric field is discontinuous at $r=R_0$. This can be seen by taking left and right limits, \begin{align} &\lim_{r\to R_0^-}E(r)=0, \\ &\lim_{r\to R_0^+}E(r)=\frac{q}{4\pi \epsilon_0 R_0^2}. \nonumber \end{align} Since electric field is continuous at all points except at $r=R_0$, there is no charge distribution except at $r=R_0$. The readers are encouraged to realize that given potential is same as the potential due to a spherical shell of radius $R_0$ having a charge $q$.