Moving Coil Galvanometer, Voltmeter, Ammeter, and their Conversions

A galvanometer has a resistance $G$ and a limiting current $i_g$. If current through the galvanometer exceeds $i_g$ then it does not work (i.e., galvanometer coil gets burnt). The value of limiting current is usually low (say a few milli Ampere).

A galvanometer can be converted to an ammeter by connecting a small resistance $S$ is parallel. This resistance is called shunt resistance. A galvanometer of resistance $G$ and limiting current $i_g$ is converted into an ammeter of measurement range zero to $i$ by connecting a resistance $S$ in parallel. The value of $S$ is given by

\begin{align} i_g G=(i-i_g)S. \end{align}

A galvanometer can be converted to a voltmeter by connecting a high resistance $R$ is series. A galvanometer of resistance $G$ and limiting current $i_g$ is converted into a volmeter of measurement range zero to $V$ by connecting a resistance $R$ in series

\begin{align} V_\text{AB}=i_g(R+G). \end{align}

Problems from IIT JEE

Problem (IIT JEE 2008): Statement 1: The sensitivity of a moving coil galvanometer is increased by placing a suitable magnetic material as core inside the coil.

Statement: Soft iron has a high magnetic permeability and cannot be easily magnetized or demagnetized.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, statement 2 is true.

Solution: The sensitivity of a moving-coil galvanometer is defined as angular deflection $\theta$ per unit current $i$. It is given as $\theta/i=nAB/k$, where $n$ is number of turns, $A$ is coil area, $B$ is magnetic field, and $k$ is torsional constant of suspension wire. To increase sensitivity, $B$ is increased by placing a soft iron core inside the coil. The soft iron has a high magnetic permeability and can be easily magnetized or demagnetized.

Problem (IIT JEE 2005): A moving coil galvanometer of resistance ${100}\;{\Omega}$ is used as an ammeter using a resistance ${0.1}\;{\Omega}$. The maximum deflection current in the galvanometer is ${100}\;{\mu A}$. Find the current in the circuit, so that the ammeter shows maximum deflection,

1. 100.1 mA
2. 1000.1 mA
3. 10.01 mA
4. 1.01 mA

Solution: 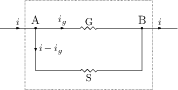A galvanometer of resistance $G$ is converted to an ammeter by connecting a small shunt resistance $S$ in parallel (see figure). Kirchhoff's loop law gives, \begin{align} &i_gG-(i-i_g)S=0,\quad \implies \quad i=i_g(G+S)/S. \nonumber \end{align} The maximum deflection current of galvanometer sets upper limit on the current measured by this ammeter. Substitute the values to get, \begin{alignat}{2} &i=i_g({G+S})/{S}=(100\times{10}^{-6})\left(({100+0.1})/{0.1})\right)={100.1}\;\mathrm{mA}. \nonumber \end{alignat}

Exercise

A voltmeter coil has resistance 50.5 $\Omega$ and a resister of 1.15 $k\Omega$ is connected in series. It can read potential differences up to 12 volts. If this same coil is used to construct an ammeter which can measure currents up to 2.0 A, what should be the resistance of the shunt used?