Series and Parallel Arrangements of Resistances

The equivalent resistance of two resistors $R_1$ and $R_2$ connected in series is given by \begin{align} R_s=R_1+R_2 \end{align}

The equivalent resistance $R_p$ of two resistors $R_1$ and $R_2$ connected in parallel is given by \begin{align} \frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2} \end{align}

The above formulas can be generalized for three or more resistors.

Solved Problems from IIT JEE

Problem from IIT JEE 2004

Six equal resistances are connected between points P, Q and R as shown in figure. Then, the net resistance will be maximum between,

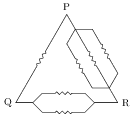
1. P and Q
2. Q and R
3. P and R
4. any two points

Solution: The equivalent resistance between P and Q, between Q and R, and between P and R are given by \begin{alignat}{2} &R_\text{PQ}=R\parallel(R/2+R/3)=R\parallel 5R/6=\frac{R (5R/6)}{R+5R/6}=\frac{5}{11}R,\nonumber\\ &R_\text{QR}=(R/2)\parallel(R+R/3)=\frac{4}{11}R,\nonumber\\ &R_\text{PR}=(R/3)\parallel(R+R/2)=\frac{3}{11}R.\nonumber \end{alignat}

Exercise

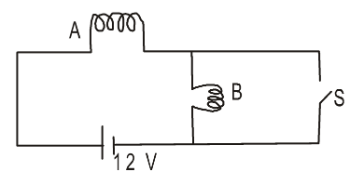
1. Two bulbs A and B are joined to a battery of 12 volts as shown in the figure. A switch S is connected as shown. Each of the two bulbs are meant to be connected to 12V source and give light corresponding to 16 watt. Initially the switch is open.

1. How much light (in watts) is emitted by A?
2. How much light (in watts) is emitted by B?
Now the switch is closed.
3. How much light (in watts) is emitted by A?
4. How much light (in watts) is emitted by B?

Experiment on series combination

When two resistors \(R_1\) and \(R_2\) are connected in series, effective resistance of the circuit becomes \(R_e=R_1+R_2\).

Procedure

You need voltmeter, ammeter, power supply, resistors and connecting wires.

You can use different kind of bulbs as resistors in this activity. Connect three resistors of resistances \(R_1\), \(R_2\) and \(R_3\) to an ammeter, a cell and a plug key, as shown in figure. The three resistors are connected in series. Close the key and note the ammeter reading. Now connect the ammeter between \(R_1\) and \(R_2\) and note the reading. Similarly, place the ammeter between the other circuit elements and measure the current. You will find that the value of the current is the same everywhere in the circuit. So, the same current passes through the three resistors.

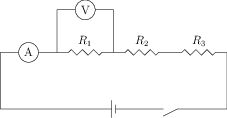
Now, connect a voltmeter in the circuit, as shown in figure. Close the key and note the potential difference \(V\) across the series combination of resistors. Then connect the voltmeter across \(R_1\) and note the reading \(V_1\). Similarly, connect the voltmeter across \(R_2\) and \(R_3\), one at a time, and measure the potential difference \(V_2\) and \(V_3\) across them. You will find that \(V=V_1+V_2+V_3\).

Experiment on parallel combination

When two resistors \(R_1\) and \(R_2\) are connected in parallel, effective resistance of the circuit becomes \(R_e=R_1R_2/(R_1+R_2)\).

Procedure

You need voltmeter, ammeter, power supply, resistors and connecting wires for this experiment.

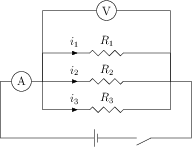
Connect three resistors (\(R_1\), \(R_2\) and \(R_3\)), an ammeter, a cell and a plug key, as shown in figure. Close the key and note the ammeter reading. This gives the current \(i\) in the circuit. Now, connect the ammeter in the branch of the circuit that has \(R_1\) and note the reading. This gives the current \(i_1\) through the branch. Similarly, place the ammeter in the branches containing \(R_2\) and \(R_3\), and measure the current \(i_2\) and \(i_3\) respectively. You will find that the current \(i\) gets divided into the branches such that \(i=i_1+i_2+i_3\).

Related

1. Electrical Resistance
2. Colour code for resistors
3. Series and Parallel Arrangements of Cells
4. Kirchhoff's Laws
5. Wheatstone bridge
6. Symmetry in electrical circuits
7. Resistance of an Electric Bulb
8. Specific resistance of the material of a wire using meter bridge and post office box
9. NAEST question on series and parallel combinations of bulbs

Subscribe to our channel