Tangent galvanometer
A tangent galvanometer consists of a magnetic needle pivoted at the centre of a circular coil. The circular coil lies in a vertical plane. The radius of the coil is very large compared to size of the needle. This ensure an approximately uniform magnetic field at the location of the needle. Also, the magnitude of the magnetic field at the location of the needle is approximately equal to the field at the coil's centre. A horizontal circular scale, graduated in degrees, is used to measure needle's deflection.
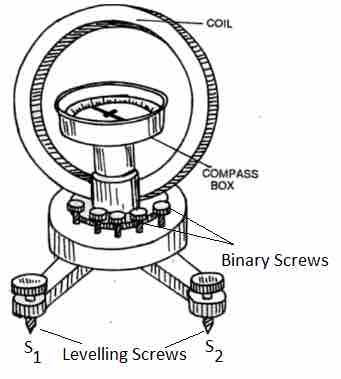
The circular coil is oriented in the vertical plane containing the magnetic meridian. The horizontal component of earth's magnetic field ($B_H$) lies in the plane of the coil. The needle's deflection is zero.
The current in the coil is switched on. The magnetic field of the coil ($B$) is perpendicular to $B_H$. The needle gets deflected by an angle $\theta$ such that \begin{align} B=B_H\tan\theta \end{align} The magnetic field of the coil of $n$ turns and radius $r$ and carrying a current $I$ is given by \begin{align} B=\frac{\mu_0 n I}{2r} \end{align} Substitute in the above equation to get \begin{align} I=\left(\frac{2B_H r}{\mu_0 n} \right)\tan\theta=K\tan\theta \end{align}
The constant $K$ is called reduction factor of the galvanometer. The current is proportional to the tangent of the needle's deflection, hence the name, tangent galvanometer.
The reduction factor $K=I$ when $\theta=45^\circ$. Thus, reduction factor of a tangent galvanometer is numerically equal to the coil's current when needle deflection is $\theta=45^\circ$.
