Motion of a Roller Made by Joining Together Two Cones

By Jitender Singh on Oct 2, 2019

This is an interesting problem from JEE Mains 2016. The problem is based on rotational motion concepts - rolling without slipping, relation between linear and angular velocity, instantaneous axis of rotation etc. The problem is explained in this short video.

Problem

A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to: (JEE Mains 2016)

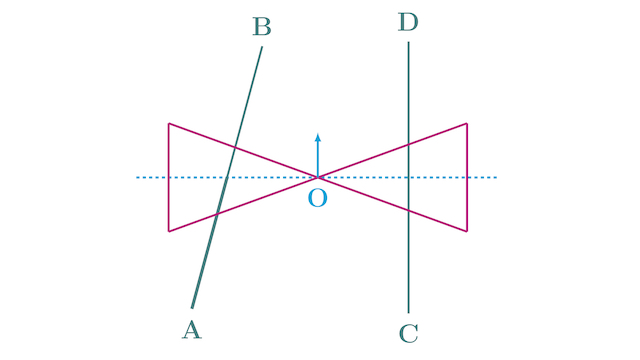
1. turn left
2. turn right
3. go straight
4. turn left and right alternately

Solution

Let the roller touches the rail AB at the point P and it touches the rail CD at the point Q (see figure). The instantaneous velocities of the roller at these points are zero because it rolls without slipping. Initially, P and Q are equidistant from the roller's axis. As the roller moves forward, the distance of P from the roller's axis ($r$) reduces because the rail AB is tilted towards O.

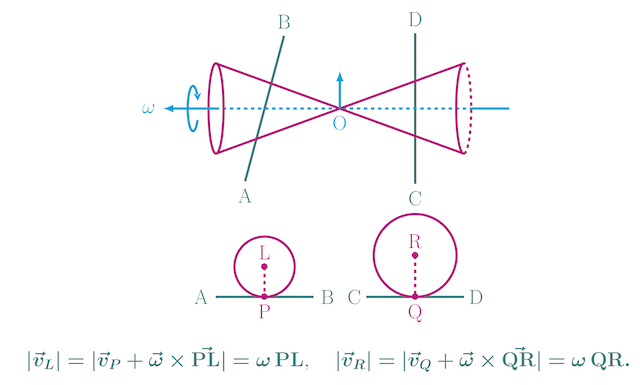
Let $\omega$ be angular velocity of the roller at some instant $t$. The distance of P from the roller axis is $r$ and that of R from the roller's axis is $r^\prime$. Thus, velocity of a point on the roller axis vertically above the rail AB is $v=\omega r$ and the velocity of a point on the roller axis vertically above the rail CD is $v^\prime=\omega r^\prime$. Since $r^\prime>r$, we get $v^\prime>v$. The point above CD moves faster than the point above AB. Hence, the roller will tend to turn left.

An analogy to this problem is a shaft connected to two wheels of unequal radii. It turn towards the smaller wheel as it moves forward.

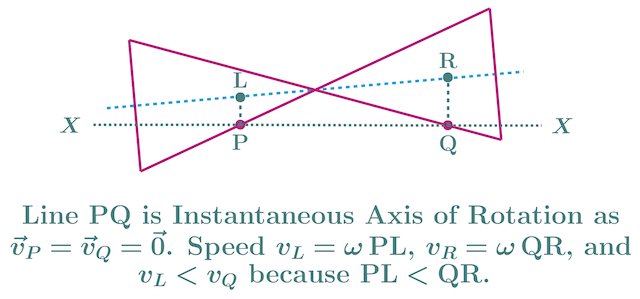
Alternate Solution based on Instantaneous Axis of Rotation

If two points on a rigid body are at rest then the line passing through these points is called the instantaneous axis of rotation. Thus, line PQ is the instantaneous axis of rotation. The speed of a point on the roller is given by the product of its angular speed and perpendicular distance from the axis of rotation. Since PL is less than QR, the speed of point L is less than that of R as we saw earlier.