Buoyancy
Problems from IIT JEE
Problem (IIT JEE 1995):
A homogeneous solid cylinder of length $L$ and cross-sectional area $A/5$ is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $L/4$ in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure $P_0$. Then, density $D$ of solid is given by,
- $\frac{5}{4}d$
- $\frac{4}{5}d$
- $4d$
- $\frac{d}{5}$
Solution:
Let A be the topmost point of the cylinder, B be the point on the interface, and C be the lowest point of the cylinder. Let the depth of point A be $h$. The pressures at A, B and C are,
\begin{align}
&P_A=P_0+hdg, \\
&P_B=P_A+\tfrac{3}{4}Ldg,\\
&P_C=P_B+\tfrac{L}{4}(2d)g\!=\!P_A+\tfrac{5}{4}Ldg.
\end{align}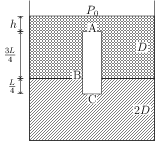
The forces on the cylinder are its weight $W=D (LA/5) g$ (downwards), hydrostatic force at the top surface $F_A=P_A (A/5)$ (downwards), and hydrostatic force at the bottom surface $F_C=P_C (A/5)$ (upwards). In equilibrium, $F_A+W=F_C$ i.e.,
\begin{align}
\label{bkb:eqn:4}
P_A A/5+D (LA/5) g=(P_A+\tfrac{5}{4}Ldg) A/5.
\end{align}
Simplify above equation to get $D={5d}/{4}$.