Parallel and Perpendicular Axes Theorems
Problems from IIT JEE
Problem (IIT JEE 1997):
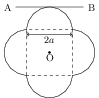 A symmetric lamina of mass $M$ consists of a square shape with a semicircular section over each of the edge of the square as shown in figure. The side of the square is $2a$. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is $1.6 M a^2$. The moment of inertia of the lamina about the tangent AB in the plane of the lamina is _____.
A symmetric lamina of mass $M$ consists of a square shape with a semicircular section over each of the edge of the square as shown in figure. The side of the square is $2a$. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is $1.6 M a^2$. The moment of inertia of the lamina about the tangent AB in the plane of the lamina is _____.
Solution:
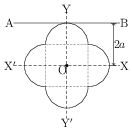 Let $\mathrm{ZZ^\prime}$ be an axis perpendicular to the lamina and passing through its centre of mass O. Given $I_\mathrm{ZZ^\prime}=1.6Ma^2$. By theorem of perpendicular axes,
\begin{align}
\label{rob:eqn:1}
I_\mathrm{XX^\prime}+I_\mathrm{YY^\prime}=I_{ZZ^\prime}.
\end{align}
By symmetry, $I_\mathrm{XX^\prime}=I_\mathrm{YY^\prime}$. Substitute in above equation to get $I_\mathrm{XX^\prime}=\frac{1}{2}I_\mathrm{ZZ^\prime}=0.8Ma^2$. The theorem of parallel axes gives,
\begin{align}
I_\mathrm{AB}=I_\mathrm{XX^\prime}+Md^2=I_\mathrm{XX^\prime}+M(2a)^2=4.8Ma^2.\nonumber
\end{align}
Let $\mathrm{ZZ^\prime}$ be an axis perpendicular to the lamina and passing through its centre of mass O. Given $I_\mathrm{ZZ^\prime}=1.6Ma^2$. By theorem of perpendicular axes,
\begin{align}
\label{rob:eqn:1}
I_\mathrm{XX^\prime}+I_\mathrm{YY^\prime}=I_{ZZ^\prime}.
\end{align}
By symmetry, $I_\mathrm{XX^\prime}=I_\mathrm{YY^\prime}$. Substitute in above equation to get $I_\mathrm{XX^\prime}=\frac{1}{2}I_\mathrm{ZZ^\prime}=0.8Ma^2$. The theorem of parallel axes gives,
\begin{align}
I_\mathrm{AB}=I_\mathrm{XX^\prime}+Md^2=I_\mathrm{XX^\prime}+M(2a)^2=4.8Ma^2.\nonumber
\end{align}
