Pressure in a Fluid

Consider an open cylindrical vessel containing a fluid of density $\rho$. The pressure at its open surface is atmospheric pressure $P_\text{atm}$. The pressure at a depth $y$ below the top surface is given by \begin{align} P=P_\text{atm}+\rho g y. \end{align} The hydrostatic pressure increases linearly with depth $y$.

The pressure difference between two horozontal layes separated by a distance $y$ is given by \begin{align} \Delta P=\rho g y. \end{align}

Problems from IIT JEE

Problem (IIT JEE 1999): A closed compartment containing gas is moving with some acceleration in horizontal direction. Neglect effect of gravity. Then, the pressure in the compartment is,

1. same everywhere
2. lower in front side
3. lower in rear side
4. lower in upper side

Solution: Let $A$ be the cross-section area and $\rho$ be the gas density. Consider a small element of width $\mathrm{d}x$ at a distance $x$ (see figure). Let pressure at the distance $x$ be $p$ and that at distance $x+\mathrm{d}x$ be $p+\mathrm{d}p$. The net force on the element due to pressure difference is, \begin{align} \mathrm{d}F & =[pA-(p+\mathrm{d}p)A] \\ &=-A\mathrm{d}p,\qquad \text{(towards right)}. \end{align}

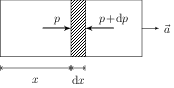
This force provides acceleration $a$ to the element. Apply Newton's second law on the element, \begin{align} -A\mathrm{d}p=ma=(\rho A \mathrm{d}x) a, \end{align} to get, \begin{align} {\mathrm{d}p}/{\mathrm{d}x}=-\rho a. \end{align} Negative sign indicates that the pressure decreases with $x$ i.e., as we go from the left to the right.