Projectiles
Projectile motion is the motion of an object that is projected into the air and then is subject to the force of gravity. It is a type of two-dimensional motion. The horizontal motion is uniform (constant velocity) and vertical motion is uniformly accelerated (free fall under gravity). The path followed by a projectile is known as the trajectory and it is a parabolic curve. The key factors that affect projectile motion are the initial velocity $u$ and the angle of projection $\theta$.
Projectile Formulas
Let a particle is projected from the origin with a velocity $u$ making an angle $\theta$ with the horizontal. The $x$ axis is in the horizontal plane (towards the direction of projection) and the $y$ axis is vertically up.
Initial velocity of the particle is \begin{align} u_x &=u\cos\theta,\\ u_y &=u\sin\theta. \end{align} The acceleration of the particle is \begin{align} a_x&=0, \\ a_y &=-g\hat\jmath. \end{align} The velocity of the particle at time $t$ is \begin{align} v_x&=u\cos\theta, \\ v_y&=u\sin\theta-gt. \end{align} The position of the particle at the time $t$ is \begin{align} x&=u\cos\theta\,t, \\ y&=u\sin\theta\, t-\tfrac{1}{2}gt^2. \end{align}
The path followed by a projectile is known as the trajectory and it is a parabolic curve. The equation of the trajectory is \begin{align} y=\tan\theta\,x-\frac{g}{2u^2\cos^2\theta}x^2. \nonumber \end{align}
The time of flight of a projectile is the amount of time it takes to travel from its launch point to the impact point. The time of flight is calculated using the following formula: \begin{align} T=\frac{2u\sin\theta}{g}. \nonumber \end{align}
The range of a projectile is the horizontal distance it travels from its launch point to the impact point. The range is calculated using the following formula: \begin{align} R=\frac{u^2\sin2\theta}{g}. \nonumber \end{align}
The maximum height of a projectile is the height of the highest point reached by the projectile during its flight. The maximum height is calculated using the following formula: and the maximum height is \begin{align} H=\frac{u^2\sin^2\theta}{2g}.\nonumber \end{align}
The range and the maximum height vary with $\theta$ as shown in the figure. The range is maximum at $\theta=45\deg$. The maximum height at this angle is $H=R_\text{max}/4$. The range and the maximum height are equal at $\theta=76\deg$.
Problem on Range of a Projectile
For angles of projection of a projectile at angles $(45^\circ-\theta)$ and $(45^\circ+\theta)$, the horizontal ranges described by the projectiles are in the ratio of
- 1:1
- 2:3
- 1:2
- 2:1
Solution: Let the projectile 1 is projected with an initial velocity $u$ at an angle of projection $\theta_1=(45^\circ-\theta)$ from the horizontal and the projectile 2 is projected with same initial velocity but at an angle of projection $\theta_2=(45^\circ+\theta)$ from the horizontal. The horizontal range of these projectiles are given by \begin{align} R_1&=\frac{u^2\sin(90^\circ-2\theta)}{g}=\frac{u^2\cos(2\theta)}{g},\nonumber\\ R_2&=\frac{u^2\sin(90^\circ+2\theta)}{g}=\frac{u^2\cos(2\theta)}{g}.\nonumber \end{align} Thus, $R_1=R_2=R$ i.e., both projectiles have same horizontal range.
The maximum heights of the two projectiles are given by \begin{align} H_1&=\frac{u^2\sin^2(45^\circ-\theta)}{2g}=\frac{u^2}{4g}\left(1-\sin2\theta\right),\nonumber\\ H_2&=\frac{u^2\sin^2(45^\circ+\theta)}{2g}=\frac{u^2}{4g}\left(1+\sin2\theta\right).\nonumber \end{align} We encourage you to show that $R=4\sqrt{H_1 H_2}$. If angle of projection of projectile 1 is $30^\circ$ and that of projectile 2 is $60^\circ$ then what is the ratio of the maximum heights of these projectiles?
The time of flight of the two projectiles are given by \begin{align} T_1&=\frac{2u\sin(45^\circ-\theta)}{g}=\frac{\sqrt{2}u}{g}\left(\cos\theta-\sin\theta\right),\nonumber\\ T_2&=\frac{2u\sin(45^\circ+\theta)}{g}=\frac{\sqrt{2}u}{g}\left(\cos\theta+\sin\theta\right),\nonumber \end{align} It is easy to show that $T_1T_2=2R/g$.
Problem on Maximum Height of a Projectile
A ball is projected from the ground with a speed 15 m/s at an angle $\theta$ with horizontal so that its range and maximum height are equal, then $\tan\theta$ will be equal to (JEE Mains 2022)
- 1/4
- 1/2
- 2
- 4
Solution: The horizontal range and the maximum height are given by \begin{align} R=\frac{u^2\sin(2\theta)}{g},\quad\text{and}\quad H=\frac{u^2\sin^2\theta}{2g}.\nonumber \end{align} Substitute in $R=H$ to get $\tan\theta=4$, which gives $\theta=\tan^{-1}(4)=76^\circ$.
Problem on Time of Flight of a Projectile
A projectile is projected with velocity of 25 m/s at an angle $\theta$ with the horizontal. After $t$ seconds its inclination with the horizontal becomes zero. If $R$ represents horizontal range of the projectile, the value of $\theta$ will be (Take $g=10\;\mathrm{m/s^2}$) (JEE Mains 2022)
- $\frac{1}{2}\sin^{-1}\left(\frac{5t^2}{4R}\right) $
- $\frac{1}{2}\sin^{-1}\left(\frac{4R}{5t^2}\right) $
- $\tan^{-1}\left(\frac{4t^2}{5R}\right) $
- $\cot^{-1}\left(\frac{R}{20t^2}\right) $
Solution: The inclination becomes zero at the maximum height. Thus, time $t$ is \begin{align} t=\frac{u\sin\theta}{g}.\nonumber \end{align} The range is given by \begin{align} R=\frac{u^2(2\sin\theta\cos\theta)}{g}.\nonumber \end{align} Eliminate $u$ from above equations and simplify to get $\cot\theta=\frac{R}{20t^2}$. The velocity $u=25\mathrm{m/s}$ is unnecessary.
Problem on Trajectory of a Projectile
The trajectory of a projectile in a vertical plane is $y=ax-bx^2$, where $a$, $b$ are constants, and $x$ and $y$ are respectively the horizontal and vertical distances of the projectile from the point of projection. The maximum height attained and the angle of projection from the horizontal are (IIT JEE 1997)
- $\frac{a^2}{b}$, $\tan^{-1} (a)$
- $\frac{a^2}{b}$, $\tan^{-1} (b)$
- $\frac{b^2}{4a}$, $\tan^{-1} (a)$
- $\frac{a^2}{4b}$, $\tan^{-1} (a)$
Solution: Trajectory equation is $y=ax-bx^2$. The slope of the trajectory is zero at maximum height i.e., \begin{alignat}{2} &\frac{\mathrm{d}y}{\mathrm{d}x}=a-2bx=0. \end{alignat} Solve above equation to get $x={a}/{(2b)}$. Substitute it in the given trajectory equation to get the maximum height \begin{align} y_\text{max}=a\left(\frac{a}{2b}\right)-b\left(\frac{a}{2b}\right)^2=\frac{a^2}{4b}. \nonumber \end{align} The slope of trajectory at the projection point is given by \begin{align} \tan\theta=\frac{\mathrm{d}y}{\mathrm{d}x}\Big|_{x=0}=a-2b(0)=a. \nonumber \end{align} Thus, the angle of projection is $\theta=\tan^{-1}(a)$.
Horizontal Projection of a Projectile
A helicopter is flying horizontally with a speed $v$ at an altitude $h$ has to drop a food packet for a man on the ground. What is the distance of helicopter from the man when the food packet is dropped? (JEE Mains 2021)
- $\sqrt{\frac{2gh}{v^2}} + h^2$
- $\sqrt{\frac{2v^2h}{g} + h^2}$
- $\sqrt{2ghv^2+h^2}$
- $\sqrt{\frac{2ghv^2+1}{h^2}}$
Solution: The time taken by the food packet to fall down a vertical distance $h$ is $t=\sqrt{2h/g}$. The horizontal distance traveled by the packet in this time is \begin{align} x=ut=u\sqrt{2h/g}.\nonumber \end{align}
The distance between the helicopter and the man at the time of release is \begin{align} d=\sqrt{h^2+x^2}=\sqrt{h^2+2hu^2/g}.\nonumber \end{align}
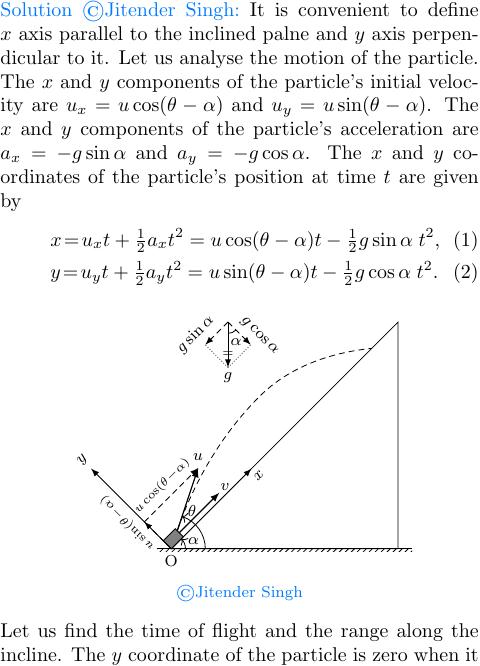
Projectile on an Inclined Plane
A frictionless inclined plane makes 45 deg angle with the horizontal. A particle is projected on the incline from the point O at an angle $\theta$ with the horizontal. Simultaneously, a box is thrown up the incline from the point O. If the particle land in the box when the box reaches its maximum height then the value of $\theta$ is?


A thought provoking problem on projectile
Question 1 A particle is projected from a point with a speed of 2 m/s at an angle 30 deg with the horizontal. The graph of the height $h$ in meters versus time in seconds is shown in the figure. What will be the angle $\theta$ shown in the figure. Neglect any air resistance.
Question 2 Suppose the particle has a positive charge $q$ and the space contains very small electric field $E$ in the upward direction. Draw $h$ vs $t$ graph (show by dotted line) in this situation on the same figure given above.
Question 3 The path of a projectile in the absence of air drag is shown in the figure by a dotted line. The path of the same projectile in the presence of air resistance is given by
- 1
- 2
- 3
- 4
