Surface Energy and Surface Tension
The surface tension of a liquid is the force per unit length applied by its surface i.e., \begin{align} S=\frac{F}{l}. \end{align} SI unit of surface tension is N/m.
Surface energy of a liquid of surface tension $S$ spread over an area $A$ is given by \begin{align} U=SA. \end{align}
Problems from IIT JEE
Problem (IIT JEE 2010):
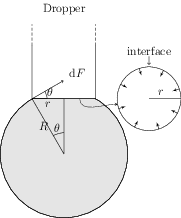
PARAGRAPH: When liquid medicine of density $\rho$ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension $T$ when the radius of the drop is $R$. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
Question 1: If the radius of the opening of the dropper is $r$, the vertical force due to the surface tension on the drop of radius $R$ (assuming $r\ll R)$ is,
- $2\pi r T$
- $2\pi R T$
- $\frac{2\pi r^2 T}{R}$
- $\frac{2\pi R^2 T}{r}$
Solution: The force due to surface tension $T$ acts on the drop-dropper interface (a circle). The direction of this force is tangential to the surface of the spherical drop (see figure). Consider a small element of length $\mathrm{d}l$ on the drop-dropper interface. The force on this element is $\mathrm{d}F=T\,\mathrm{d}l$, and it makes an angle $\theta$ from the horizontal. Resolve $\mathrm{d}F$ in the horizontal and the vertical directions to get, $\mathrm{d}F_\text{h}=T\,\mathrm{d}l\,\cos\theta$ and $\mathrm{d}F_\text{v}=T\,\mathrm{d}l\,\sin\theta$. By symmetry, the force $\mathrm{d}F_\text{h}$ on two diametrically opposite elements on circular interface is equal and opposite. Thus, total force in the horizontal direction, $F_\text{h}=\int\mathrm{d}F_\text{h}=0$. Integrate the vertical component over the circular interface to get $F_\text{v}=T(2\pi r)\sin\theta=2\pi r T (r/R)=2\pi r^2 T/R$. Hence, correct answer is C.
Question 2: If $r={5\times{10}^{-4}}\;\mathrm{m}$, $\rho={{10}^{3}}\;\mathrm{kg/m^3}$, $g={10}\;\mathrm{m/s^2}$, $T={0.11}\;\mathrm{N/m}$, the radius of the drop when it detaches from the dropper is approximately,
- $1.4\times{10}^{-3}\;\mathrm{m}$
- $3.3\times{10}^{-3}\;\mathrm{m}$
- $2.0\times{10}^{-3}\;\mathrm{m}$
- $4.1\times{10}^{-3}\;\mathrm{m}$
Solution: The drop will detach from the dropper when its weight is equal to the vertical force due to surface tension i.e., \begin{align} (4/3)\pi R^3\rho g=2\pi r^2 T/R. \end{align} Solve above equation to get, \begin{align} R & =\left[3r^2 T/(2\rho g)\right]^{1/4} \\ &\approx {1.4\times{10}^{-3}}\;\mathrm{m}.\nonumber \end{align} Hence, correct answer is A.
Question 3: After the drop detaches, its surface energy is,
- $1.4\times{10}^{-6}\;\mathrm{J}$
- $2.7\times{10}^{-6}\;\mathrm{J}$
- $5.4\times{10}^{-6}\;\mathrm{J}$
- $8.1\times{10}^{-6}\;\mathrm{J}$
Solution: The surface energy of the spherical drop of radius $R$ is given by, \begin{align} U &=T(4\pi R^2) \\ &=(0.11)4\pi(1.4\times{10}^{-3})^2 \\ &={2.7\times{10}^{-6}}\;\mathrm{J}.\nonumber \end{align} Hence, answer is B.
