Thought provoking problems on Mechanics

By Jitender Singh on Dec 3, 2022

These problems are from pre-test conducted in teacher's workshops by Prof HC Verma and his team.

Test 1

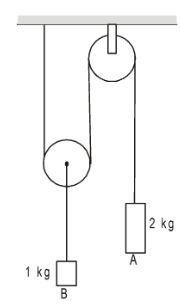
1. In the situation shown in the figure, the rope is light and the pulleys are frictionless. (a) Find the acceleration of the blocks A and B. Will the pulleys rotate clockwise, anticlockwise or will not rotate?

2. A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
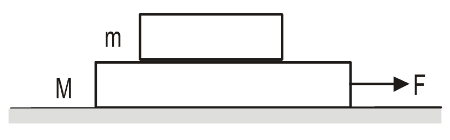
3. A block of mass $m$ is kept on another block of mass $M$ and the system rests on a horizontal surface. A constant horizontal force $F$ acting on the lower block produces an acceleration $\frac{F}{2(m+M)}$ in the system, the two blocks always move together.
1. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.

2. Find the frictional force acting on the smaller block.
3. Find the kinetic energy of the smaller block as it moves a distance $d$.
4. Find the work done by the force of friction on the smaller block during a displacement of the system.
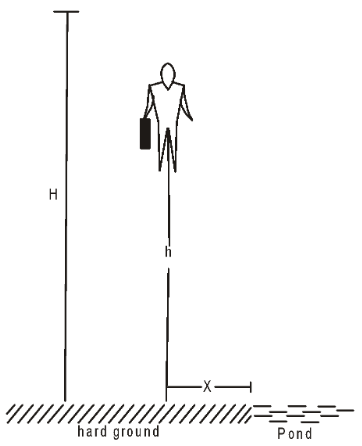
4. A man of mass $M$ having a bag of mass $m$ slips from the roof of a tall building of height $H$ and starts falling vertically. When at a height $h$ from the ground, he notices that the ground below him is pretty hard, but there is a pond at a horizontal distance $x$ from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?

Test 2

1. Newton's second law is $F=ma$. When you push a wall, it does not move. That means, the applied force $F\neq 0$ but the acceleration is zero. Why this is not a violation of Newton's laws?
2. A small rubber ball is released at $t=0$ from a height $H$ above a hard floor. The ball hits the ground and in a very short time it rebounds and goes vertically upwards to reach the same height $H$. Take positive $x$-direction to be upward. For this entire period plot
1. Position $x$ versus time $t$ graph
2. Velocity $v$ versus time $t$ graph
3. Acceleration $a$ versus time $t$ graph
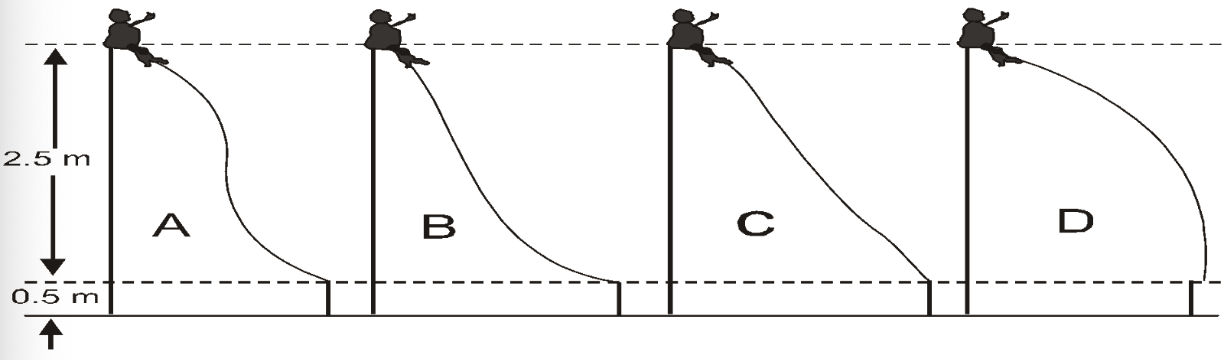
3. A young girl wishes to select one of the frictionless playground slides illustrated below to give her the greatest possible speed when she reaches the bottom of the slide. Which of the slides illustrated in the diagram above should she choose?

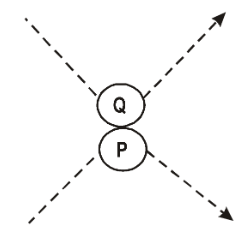
4. The diagram depicts the paths of two colliding steel balls, P and Q.

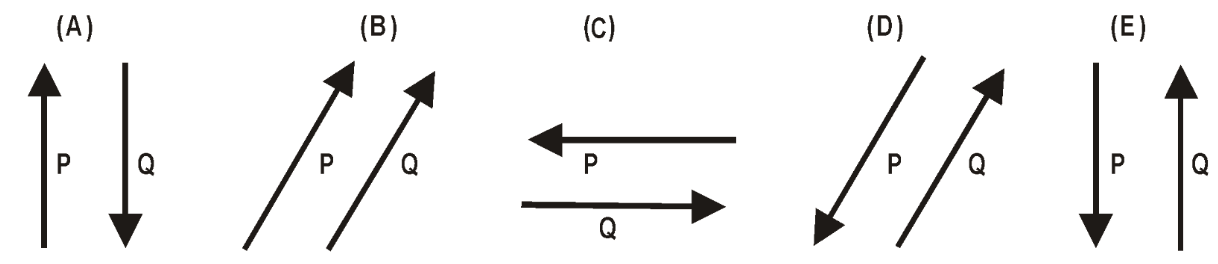
1. Which set of arrows best represents the direction of the change in momentum of each ball?

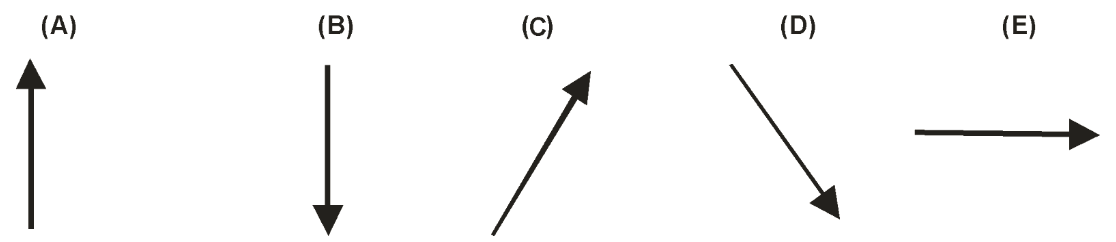
2. Which arrow best represents the direction of the impulse applied to ball Q by ball P during the collision?

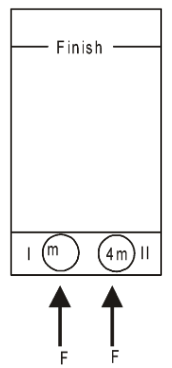
5. The diagram depicts two blocks on a frictionless table. Block II is four times as massive as block I. Starting from rest, the blocks are pushed across the table by two equal forces. Giving short explanations answer the following.

1. Which block will have the greater kinetic energy upon reaching the finish line?
2. Which block will reach the finish line first?
3. Which block will have the greater linear momentum upon reaching the finish line?
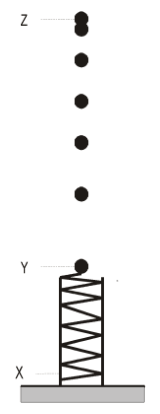
6. The figure represents a multiflash photograph of a small ball being shot straight up by a spring. The spring, with tha ball atop, was initially compressed to the point marked X and released. The ball left the spring at the point marked Y, and reaches its highest point at the point marked Z. Assume that air resistance is negligible. Mark the following statements as TRUE or FALSE.

1. The acceleration of the ball was greatest just before it reached point Y (still in contact with the spring).
2. The acceleration of the ball was decreasing on its way from point Y to point Z.
3. The acceleration of the ball was zero at point Z.
4. The acceleration of the ball was the same for all points in its trajectory from points Y to Z.
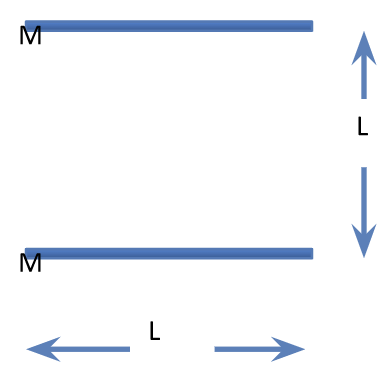
7. Consider two rods A and B each of mass $M$ and length $L$. They are placed parallel to each other at a separation $L$. What can you say about the direction and the magnitude of the gravitational force acting due to the rod A on the rod B?

Test 3

1. A particles of mass $m$ capable to move on the $x$-axis is subjected to a force $F(x)=-k(x-A)$, where $k$ is a positive constant. At $t=0$, the particle is at $x=B$ and its velocity is $v=0$. Find the expression of its position at time $t$.
2. Consider a system of 5 particles. The total mass, total kinetic energy and total linear momentum of the system at $t=0$ are $m$, $P_0$ and $K_0$ as seen from the lab frame. Now look at the system from a frame moving with a velocity $\frac{P}{2M}$ with respect to the lab frame. What is the linear momentum $P^\prime$ and kinetic energy $K^\prime$ of the system as seen from this frame?
3. Two blocks moving along a line collide. The collision is partially inelastic so that the kinetic energy decreases by $\Delta K$ as seen from the lab frame. The collision is seen from another inertial frame, moving with respect to the lab with a constant velocity $v_0$. Will the loss in kinetic energy during collision as seen from this frame be same as, more or less than $\Delta K$?
4. A particle is dropped from a height H over a hard horizontal surface. As it collides with the surface and rebounds, the speed becomes half of the speed before the collision. Draw a height versus time graph from the time it was dropped till its third collision with the surface. Make sure that scales are drawn on the axes and the graph is to the scale as far as you can.

Test 4

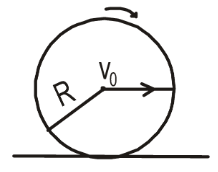
1. A ring of radius $R$ is rolling without slipping on a horizontal surface as suggested in the figure. The linear speed of the center is $v_0$. Find the part of the ring for which the linear speed of the particles is less than or equal to $v_0$.

2. The net force acting on a rigid body is zero. Mark True/False.
1. The linear momentum of the body must remain constant.
2. The angular momentum of the body must remain constant.
3. The net force acting on a rigid body is NOT zero. Mark True/False
1. The momentum of the rigid body must change with time.
2. The angular momentum of the rigid body must change with time.
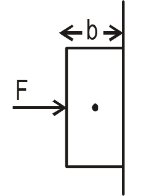
4. A uniform rectangular block of mass $M$ and width $b$ is pushed against a vertical wall by applying a horizontal force $F$ passing through the center of mass (see the figure). The block remains at rest. Find the torque, about the center of mass of block, of

1. The applied force
2. the frictional force on the block
3. the normal force on the block
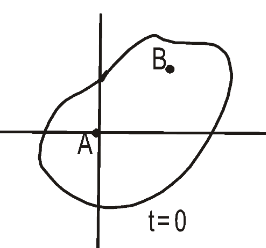
5. A rigid body is making mixed translational and rotational motion. At time $t=0$, a particle A of the rigid body is at the origin and another particle B is at (3,4,0). After some time the particle A is at (5,5,0). Which of the following is (are) possible position(s) of the particle B at this time?

1. (10, 5, 0)
2. (5, 10, 0)
3. (8, 9, 0)
4. (9,8,0)
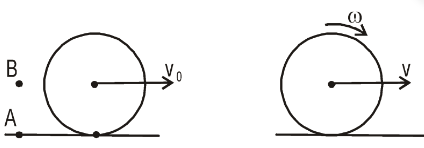
6. A sphere lying on a rough surface is given a translational velocity $v_0$ but no angular velocity. Because of friction from the surface, the velocity of the center decreases and the sphere picks up an angular velocity and finally it starts rolling without slipping. A is a fixed point on the line of motion of the point of contact and B is a fixed point on the line of motion of the center of mass. Angular momentum of the sphere is
1. constant about the center of the sphere
2. constant about A
3. constant about B
4. not constant about any of these points.

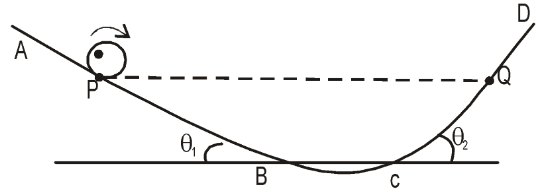
7. A track ABCD has parts AB and CD as inclined planes of angles $\theta_1$ and $\theta_2$ respectively joined smoothly to the curved part BC. A ball of mass $m$ rolls without slipping on the track. It starts ($v=0$) from a place P on AB and reaches up to point Q on CD.

1. Is the height of Q same as, less than or more than that of P?

2. What are the directions of friction when the ball is on part AB and is on part CD?
3. Are the component of acceleration in vertically downward same or different in the two cases? If different, in which case it is more?
8. A solid sphere is put at the top of a smooth incline of angle $\theta$. Mark the following statements as TRUE or FALSE.
1. The sphere will roll down for small $\theta$ and slide down only for $\theta$ greater than a certain non-zero value.
2. The sphere will remain at rest for small $\theta$ and roll down only for $\theta$ greater than a certain non-zero value.
3. The sphere will slide down for all $\theta > 0$ deg.
4. The sphere will roll down for all $\theta > 0$ deg.