Young's Modulus
The ratio of longitudinal stress to the longitidunal strain is called Young's modulus i.e., \begin{align} Y=\frac{F/A}{\Delta l/l}=\frac{Fl}{A\Delta l} \end{align} The unit of Young's modulus is N/m2 or Pascal. Young's modulus and the pressure have the same unit.
Young's modulus by bending of beam
If a beam rests horizontally on two fixed points and is loaded at middle, it sags. The load $mg$, Length $l$ between the fixed supports, width $b$ of the beam, thickness $d$ of the beam and the Young’s modulus $Y$ of the material are related by \begin{align} Y=\frac{mgl^3}{4zbd^3} \end{align} Here $z$ is the depression of middle point of the beam.
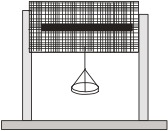
- Take a 30 cm plastic scale. This is to be used as a beam.
- Measure the width of the scale using another plastic scale. Measure the thickness of the middle portion using a Screw gauge. Write your data in a neat tabular form.
- Make it to rest on two supports. The scale should be horizontal as well as stable. A pan is hanging from the middle of the scale. Check that a sharp pointer is attached to the scale at middle. Put 50 gm weight on the pan.
- Measure the length between the points of the support where the scale rests on them.
- A graph paper is pasted on a vertical card board. Make sure that tip of the pointer almost touches the graph paper. Note the position of the tip on the graph paper.
- Now increase the weight in steps of 50 gm and each time wait till the depression reaches its maximum. Note the depression for each weight till the total weight goes to 400 gm.
- Now decrease the weight in steps and again note the depression for each weight after waiting for appropriate time. Write all your data in nicely formatted tables.
- Find the average depression for each weight.
- Plot a graph between $z$ and the mass $m$.
- Calculate the slope $\frac{gl^3}{4bYd^3}$ and from this find the Young modulus of the plastic scale.
Problems from IIT JEE
Problem (IIT JEE 2015): In plotting stress versus strain curves for two materials P and Q, a student by mistake puts strain on the $y$-axis and stress on the $x$-axis as shown in the figure. Then the correct statement(s) is(are),
- P has more tensile strength than Q.
- P is more ductile than Q.
- P is more brittle than Q.
- The Young's modulus of P is more than that of Q.
Solution: The tensile strength of a material is generally defined as the stress at which the material breaks. From the figure, P has more strength than Q (because $S_\text{P}>S_\text{Q}$).
The material Q is brittle because its stress-strain curve does not show any yield. The material P is ductile as its stress-strain curve clearly show yielding (the part beyond the small kink). Thus, P is more ductile than Q. In the elastic region (straight line portion), the slope of P is more than that of Q i.e., \begin{align} &\left(\frac{\text{strain}}{\text{stress}}\right)_P > \left(\frac{\text{strain}}{\text{stress}}\right)_Q &&\text{i.e.,} \\ &\left(\frac{\text{stress}}{\text{strain}}\right)_P < \left(\frac{\text{stress}}{\text{strain}}\right)_Q.\nonumber \end{align} Thus, Young's modulus of P is less than that of Q.
