Alpha, Beta and Gamma Radiations
By Alpha, beta, and gamma radiation are ionizing radiation emitted by unstable nuclei as they undergo radioactive decay.
- Alpha Radiation is composed of alpha particles (Helium nucleus). Alpha particles have low penetration power because of their relatively large size and mass.
- Beta Radiation is composed of high-energy electrons that are emitted by the nucleus during radioactive decay. Beta particles are smaller and lighter than alpha particles and have greater penetration power. They can be stopped by a sheet of metal or thick plastic.
- Gamma Radiation is a type of high-energy electromagnetic radiation that is emitted by the nucleus during radioactive decay. Gamma rays are similar to X-rays in their properties and can penetrate through several centimeters of dense materials, making them difficult to shield. Gamma rays are highly ionizing and can cause significant damage to living tissues.
Problems from IIT JEE
Problem (IIT JEE 2012):
PARAGRAPH: The $\beta$-decay process, discovered around 1900, is basically the decay of a neutron $(n)$. In the laboratory, a proton $(p)$ and an electron $(e^-)$ are observed as the decay product of the neutron. Therefore, considering the decay of a neutron as a two body decay process, it was predicted theoretically that the kinetic energy of the electron should be constant. But experimentally, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process i.e., $n\rightarrow p+e^- +\bar{\nu}_e$, around 1930, Pauli explained the observed electron energy spectrum. Assuming the antineutrino ($\bar{\nu}_e$) to be massless and possessing negligible energy, and the neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is ${0.8\times{10}^{6}}\;\mathrm{eV}$. The kinetic energy carried by the proton is only the recoil energy.
Question 1: What is the maximum energy of the anti-neutrino?
- Zero.
- Much less than ${0.8\times{10}^{6}}\;\mathrm{eV}$.
- Nearly ${0.8\times{10}^{6}}\;\mathrm{eV}$.
- Much larger than ${0.8\times{10}^{6}}\;\mathrm{eV}$.
Solution:
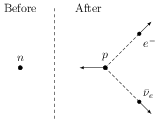The energy released in $\beta$-decay is given by,
\begin{align}
Q&=\left[m_n-(m_p+m_e+m_{\bar{\nu}_e})\right]c^2\nonumber\\
&=\left[m_n-(m_p+m_e)\right]c^2 \quad (\because m_{\bar{\nu}_e}=0). \nonumber
\end{align}
This energy is in the form of kinetic energy of released particles i.e.,
\begin{align}
Q&=K_p+K_e+K_{\bar{\nu}_e} \approx K_e+K_{\bar{\nu}_e}\qquad (\because K_p\approx 0).\nonumber
\end{align}
The conservation of linear momentum gives,
\begin{align}
\vec{p}_p+\vec{p}_e+\vec{p}_{\bar{\nu}_e}=0.\nonumber
\end{align}
The $K_e$ is maximum when $K_{\bar{\nu}_e}=0$ (and hence $p_{\bar{\nu}_e}=0$). This is possible in three body decay without violating momentum conservation. Thus,
\begin{align}
Q=K_{e}^\text{max}={0.8\times{10}^{6}}\;\mathrm{eV}.\nonumber
\end{align}
Similarly, $K_{\bar{\nu}_e}$ is maximum when $K_{e}=0$ i.e.,
\begin{align}
K_{\bar{\nu}_e}^\text{max}=Q={0.8\times{10}^{6}}\;\mathrm{eV}.\nonumber
\end{align}
Question 2: If the anti-neutrino had a mass of ${3}\;\mathrm{eV/c^2}$ (where $c$ is the speed of light) instead of zero mass, what should be the range of the kinetic energy, $K$, of the electron?
- $0 \leq K \leq {0.8\times{10}^{6}}\;\mathrm{eV}$
- ${3.0}\;\mathrm{eV} \leq K \leq {0.8\times{10}^{6}}\;\mathrm{eV}$
- ${3.0}\;\mathrm{eV} \leq K < {0.8\times{10}^{6}}\;\mathrm{eV}$
- $0 \leq K < {0.8\times{10}^{6}}\;\mathrm{eV}$
Solution: If $m_{\bar{\nu}_e}={3}\;\mathrm{eV/c^2}$, then, \begin{align} Q={0.8\times{10}^{6}}\;\mathrm{eV}-{3}\;\mathrm{eV} < {0.8\times{10}^{6}}\;\mathrm{eV}.\nonumber \end{align} Thus, $K_{\bar{\nu}_e}^\text{max}=Q < {0.8\times{10}^{6}}\;\mathrm{eV}$. The $K_{\bar{\nu}_e}^\text{min}$ is related to $p_{\bar{\nu}_e}^\text{min}$ which can be zero in three body decay making $K_{\bar{\nu}_e}^\text{min}=0$.
Problem (IIT JEE 2001): The electron emitted in beta radiation originates from
- inner orbits of atom.
- free electrons existing in nuclei.
- decay of a neutron in a nucleus.
- photon escaping from the nucleus.
Solution: Beta rays are the electrons emitted by the nucleus when a neutron is converted to a proton $\sideset{_0^1}{}{n}\to \sideset{_1^1}{}{p}+\sideset{_{-1}^{\;\; 0}}{}{e}$.
Problem (IIT JEE 1999) Which of the following is a correct statement?
- Beta rays are same as cathode rays.
- Gamma rays are high energy neutrons.
- Alpha particles are singly ionized helium atoms.
- Protons and neutrons have exactly the same mass.
The $\beta$ particles are electrons emitted by the nucleus whenever a neutron is converted to a proton. The gamma rays are electromagnetic radiations. Alpha particle is doubly ionized helium atom. The rest mass of a neutron is slightly greater than that of a proton.
