Thomson method to determine e/m of an electron
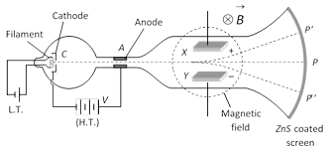
The charge to mass ratio ($e/m$) of an electron was experimentally determined by J.J. Thomson. The experimental set-up consists of a cathode ray tube which has three parts:
- The electron gun: This consists of a cathode and an anode. It produces, accelerates, and focuses the electrons into a fine beam.
- The screen: The screen is coated with fluorescent material like zinc sulphide (ZnS) so that a visible spot is observed when electron beam strikes the screen.
- The electric and magnetic deflecting system: Two plates are fitted in the tube symmetrically on either side of the electron beam so that electric field perpendicular to the plane of the paper can be applied. A magnetic field can also be applied at the same place in a direction perpendicular to the direction of the electric field i.e., in the plane of the paper. Thus, the deflection of the cathode rays due to the electric as well as the magnetic field takes place in a direction perpendicular to the plane of the paper.
The electric force on the electron of charge $e$ in the electric field $E$ is $F_E=eE$.
When magnetic field $B$ is applied, the electron beam is deflected. If $v$ is the velocity of the electrons in the beam, then magnitude of the magnetic force on the lectron is $F_B=evB$. As magnetic force acts perpendicular to the direction of motion of the lectron, the electron moves along a circular path in the magnetic field and on leaving the field flies off tangentially meeting the screen.
If $r$ is the radius of the circular path along which the electron moves in the magnetic field,then \begin{align} evB=\frac{mv^2}{r} \end{align}
To find the velocity $v$, one of the fields say the magnetic field is first applied. The spot of light moves from its initial position to the position say M. The electric field is now applied simultaneously so as to produce deflection of the electron beam in the opposite direction. The value of electric field is so adujusted that the spot of light comes back to its initial position. In such a case the forces acting on the electron due to the electric and magnetic fields are equal and opposite, $eE=evB$, which gives \begin{align} v=\frac{E}{B} \end{align}
Substitute in the above equation to get \begin{align} \frac{e}{m}=\frac{E}{rB^2} \end{align}
The radius of the path is determined by the electrons path. Let $y$ be the distance moved on the screen, $l$ be length of the plates and $L$ be distance of the screen from the plates then \begin{align} r=\frac{Ll}{y} \end{align} If $V$ is the potential difference applied between the plates and $d$ is separation between the plates then the electric field between the plates is given by $E=V/d$.
The charge to mass ratio is given by \begin{align} \frac{e}{m}=\frac{yV}{LldB^2} \end{align}
