Convex lens
Convex lens is a spherical lens. Its focal lens is related to radius of curvature and refractive index of the lens material. The focal length is given by lens maker's formula \begin{align} \frac{1}{f}=(\mu-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right] \end{align}
Find approx focal length of a convex lens
A convex lens converges rays parallel to its axis on its focus. The distance between the pole of the lens and its focus is called focal length of the lens.
Take a convex lens. You can also use a magnifying glass. Face the lens towards the sun. Take a small block of wood and place it close to the lens such that the lens is between the sun and the block. Slowly move the lens away from the block. At one stage, a very small, bright image will be formed on the block. The distance between the lens and the block in this position is the focal length of the convex lens.
This method does not work for concave lenses. A concave lens forms a virtual image which cannot be captured on a screen such as your wooden block. Other methods are used to find its focal length.
Nature of image formed by a convex lens
In this activity we will use the convex lens of a magnifying glass. First find the approximate focal length (\(f\)) of the lens. Then fix it vertically on a stand. Draw a long straight line on a table and place the lens stand on it. The principal axis of the lens should be parallel to and exactly above the line on the table. On one side of the stand mark the points \(F_1\) and \(2F_1\) on the line, at distance \(f\) and \(2f\) respectively from the lens. Similarly, mark \(F_2\) and \(2F_2\) on the other side of the stand.
You need a convex lens, screen, lens stand, candle, and a scale
Make a small screen of stiff paper and fix it on the stand. The screen should be vertical, with its centre at about the same height as the principal axis of the lens. Place the screen stand on the line drawn on the table.
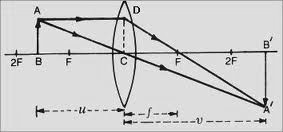
Light a candle and place it on the line such that the lens is between the candle and the screen. The flame of the candle should be at about the same height as the principal axis of the lens. Move the screen back and forth till you see a sharp image of the flame on the screen. Repeat this by placing the candle at different positions. In each case note the size of the image. Try to see the image properties for different locations of the object. In which cases are the image not formed on the screen?
Verification of lens formula
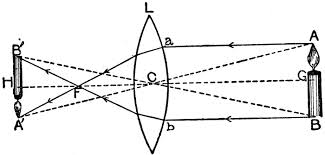
The object distance \(u\), image distance \(v\), and the focal length \(f\) of the lens are related by,
\begin{align} \frac{1}{v}-\frac{1}{u}=\frac{1}{f}. \nonumber \end{align}The pole of the lens is taken as the origin and principal axis as the \(X\)-axis. Usually, the positive of the axis is taken along the incident rays. The distance between the pole and the object (candle) is \(u\) and the distance between the pole and the image (screen) is \(v\). Note that \(u\) is negative and \(v\) is positive in present case.
You need a convex lens, V-stand, screen, screen-stand, candle, matchbox, and a scale.
- Firstly, find the approximate focal length \((f)\) of the convex lens. Then fix it vertically on a V-stand. Draw a long straight line on a table and place the lens in the middle. The pole of the lens should be exactly above the line.
- Light a candle and place it on one end of the line. The flame of the candle should be at the same height as the pole of the lens.
- Fix the screen on its stand. The screen should be vertical. Place the screen on other side of the lens.
- Analyse the nature of the image by moving the screen and/or lens.
- For three different values of \(u\), find the value of \(v\). Calculate \(f\) by substituting in formula given above.
Divergence by a convex lens
Convex lens is known for converging a beam of light.
Take a laser torch and direct it towards a distant wall or a roof. Laser goes as a parallel beam and make a spot of small size. Now, ask the audience what will happen to the spot if we bring a convex lens in between the laser torch and the spot. The general reply is that the beam will converge and spot size will be reduced.
Now, take a convex lens and put it in front of the laser torch. The spot size will increase and the audience will feel that beam is diverging.
As is clear from the figure, if the wall is too far away from the lens, the spot size will become larger. The lens converges the parallel beam to its focus and beyond the focus the rays continues and hence spot becomes larger.
Convex lens in water
This experiment is to study the effect of water surrounding the lens on its focal length.
The focal length of a lens depends on the curvature of the two lens surfaces and on the refractive indices of the lens and surrounding medium. The equation for focal length of a lens is given by lens maker's formula,
\begin{align} \frac{1}{f}=\left(\frac{\mu_2}{\mu_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\nonumber \end{align}where \(\mu_2\) and \(\mu_1\) are refractive indices of the lens and surrounding medium, respectively. Thus, if the lens is kept inside water instead of air, its focal length will increase.
You need two laser torch, a long trough, convex lens of focal length about 10 cm or less.
Take a convex lens and measure its focal length (approximately) by imaging distant object on the wall or a paper. Choose a lens of short focal length, preferable 10 cm or less. Put water in a long trough made of transparent plastic box and put a few drops of soap solution in it. Take two laser torches and fix them on same base, parallel to each other. Position the laser base so that light may go in water along the length of the trough. Switch on both the lasers. The laser beams will go in the water. The beams will be clearly visible from the top. The beams are quite narrow and you can treat each of these as ray of light.
Put the convex lens inside the water so that the axis is parallel to the beams of light. You can ask audiences to hold the lens from the top, so that it stays there. The two beams will bend towards each other and will intersect. Ask a volunteer from the audience to measure the distance of the lens from the place where the two beams intersect.
Measured distance is focal length of the lens in water. Check that the focal length in water is much more than the focal length in air.
Related
Subscribe to our channel
