Deviation by a Prism
The path of a light ray gets deviated when it passes through a prism. It occurs due to refraction of light at prism's two non-parallel faces.
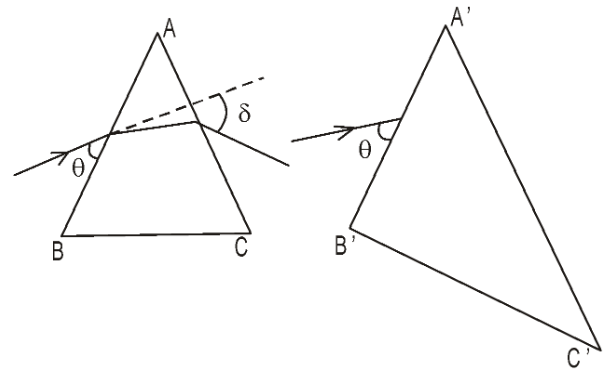
The deviation angle of a prism is the angle between the incident and refracted rays after passing through the prism. The deviation angle $\delta$ is related to the prism angle $A$ by \begin{align} \delta= i+i^\prime-A \end{align}
The angle of deviation $\delta$ varies with angle of incidence $i$. It attains a minimum value for a specific value of $i$. At the condition of minimum deviation, $i=i^\prime$, and \begin{align} \mu=\frac{\sin\frac{A+\delta_m}{2}}{\sin\frac{A}{2}} \end{align}
If prism angle is small then above equation can be approximated as \begin{align} \delta_m=(\mu-1)A. \end{align}
Demo of minimum deviation by a prism
When light falls on a surface of a prism with an angle of incidence more than a certain angle (nearly 30 degree for a 60 degree - 60 degree prism) it comes out after two refraction. The angle of deviation \(\delta\) changes with angle of incidence \(i\). As the angle of incidence is increased from 0 degree to 90 degree the angle of deviation \(\delta\) first decreases, acquires a minimum value, and then increase again. The value of minimum deviation \(\delta_m\) is related to the refractive index of the prism.
Put a prism on a cylindrical box (or an inverted glass) and set a laser torch in a stand so that it can send light to nearly the middle portion of a rectangular face of the prism. Remove the prism from the box and put on the laser. Locate the spot of the laser on the wall and mark the position of the spot on the wall. This represents the direct beam.
Now, hold the box in your hand and place the prism over it so that laser beam strikes one of the rectangular face of the prism. Rotate the box so that light enters through one of the rectangular surface and comes out through the second surface. The spot will be deviated on the wall. Now, slowly rotate the box about the vertical axis. Check if the spot goes towards the original direct position. If it goes away from the original direct position, rotate the box in opposite direction. Keep rotating the box in this direction slowly and try to bring the spot as close to the direct position as possible.
You will find that the spot cannot be brought closer than a particular amount. This is the minimum deviation position.
Exercise
- In the figure, two prisms are shown, $AB\parallel A^\prime B^\prime$ and $AC\parallel A^\prime C^\prime$. Light rays fall on $AB$ and $A^\prime B^\prime$ at the same angle. The angle of deviation $\delta$ in case (i) is the minimum possible deviation.
- Is the angle of deviation in case (ii) equal to $\delta$
- Is the angle of deviation in case (ii) minimum deviation or not?