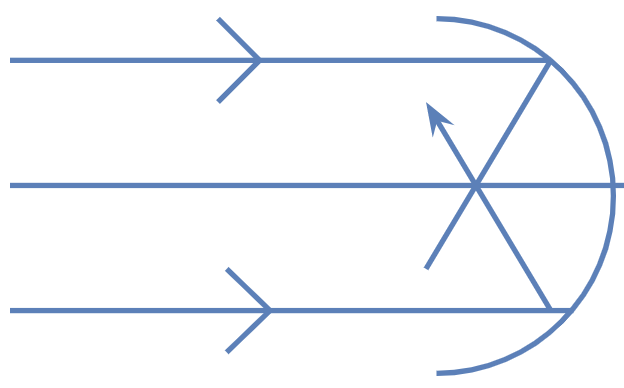
Reflection from Spherical Mirrors
There are two laws of reflection
- Incident ray, reflected ray, and normal lie in the same plane
- The angle of incidence $i$ is equal to the angle of reflection $r$ i.e., $\angle i=\angle r$
The focal length of a spherical mirror of radius of curvature $R$ is given by \begin{align} f=R/2 \end{align}
The object distance $u$, the image distance $v$ and the focal length $f$ are related by the mirror formula \begin{align} \frac{1}{v}+\frac{1}{u}=\frac{1}{f} \end{align}
The magnification by a spherical mirror is given by \begin{align} m=-\frac{v}{u} \end{align}
Exercise
- A small dog is running with a constant velocity of 1m/s along the principle axis of a convex mirror of focal length 20cm. Plot a graph of the velocity with which the image moves w.r.t time. Consider that the dog moves from a 5 metre distance from the mirror and reaches a distance equal to the focal length of the mirror.
- The figure shows a new shiny hemispherical vessel and two light rays parallel to the symmetry axis. They meet at 10 cm from the pole after reflection. The rays are incident near the edge of the vessel. Should the radius of the hemisphere be equal to 20 cm, greater than 20 cm or smaller than 20 cm?