Thin Lenses
Let a spherical surface of radius $R$ separates two media of refractive indices $\mu_1$ and $\mu_2$. The object distance $u$ and the image distance $v$ are related by
\begin{align} \frac{\mu_2}{v}-\frac{\mu_1}{u}=\frac{\mu_2-\mu_1}{R}, \end{align} and the image magnification is given by \begin{align} m=\frac{\mu_1 v}{\mu_2 u}. \nonumber \end{align}Consider a lens made from a material of refractive index $\mu$. It has two spherical surfaces of radii of curvature $R_1$ and $R_2$. The focal length $f$ of this lens is given by Lens Maker's formula \begin{align} \frac{1}{f}=(\mu-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right] \end{align}
The lens formula relates object distance $u$, image distance $v$ and the focal length $f$ by \begin{align} \frac{1}{v}-\frac{1}{u}=\frac{1}{f}. \end{align} The magnification by the lens is given by \begin{align} m=\frac{v}{u}. \end{align} The power of a lens of focal length $f$ is given by \begin{align} P=\frac{1}{f}. \end{align} The power $P$ is in diopter if $f$ is in metre.
Let two thin lenses of focal lengths $f_1$ and $f$ are separated by a distance $d$. The focal length $F$ of the combination is given by \begin{align} \frac{1}{F}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{d}{f_1f_2}. \end{align}
Problems from IIT JEE
Problem (IIT JEE 2010): The focal length of a thin biconvex lens is 20 cm. When an object is moved from a distance of 25 cm in front of it to 50 cm, the magnification of its image changes from $m_{25}$ to $m_{50}$. The ratio $\frac{m_{25}}{m_{50}}$ is,
Solution: The lens formula, $1/v-1/u=1/f$, for the two locations of the object gives, \begin{align} \frac{1}{v_1}-\frac{1}{-25}=\frac{1}{20},\\ \frac{1}{v_2}-\frac{1}{-50}=\frac{1}{20}. \end{align} The first equation gives $v_1={100}\;\mathrm{cm}$ and second equation gives $v_2={100/3}\;\mathrm{cm}$. Thus magnification in the first case is $m_{25}=v_1/u_1=-4$ and that in the second case is $m_{50}=v_2/u_2=-2/3$. Hence, $m_{25}/m_{50}=6$.
Problem (IIT JEE 1997): Two thin lenses, when in contact, produce a combination of power $+10\,D$. When they are 0.25 m apart, the power reduces to $+6\,D$. The focal length of the lenses are ______ m and _______ m.
Solution: The effective focal length of two thin lenses of focal length $f_1$ and $f_2$ in contact is, \begin{align} \label{qvb:eqn:1} {1}/{F}={1}/{f_1}+{1}/{f_2}, \end{align} and that for lenses separated by a distance $d$ is, \begin{align} \label{qvb:eqn:2} {1}/{F^\prime}={1}/{f_1}+{1}/{f_2}-{d}/{(f_1 f_2)}. \end{align} Substitute ${1}/{F}={10}\;\mathrm{m^{-1}}$ in first equation, ${1}/{F^\prime}={6}\;\mathrm{m^{-1}}$ and $d={0.25}\;\mathrm{m}$ in second equation and then solve to get $f_1={{1}/{8}}\;\mathrm{m}$ and $f_2={{1}/{2}}\;\mathrm{m}$.
Exercise
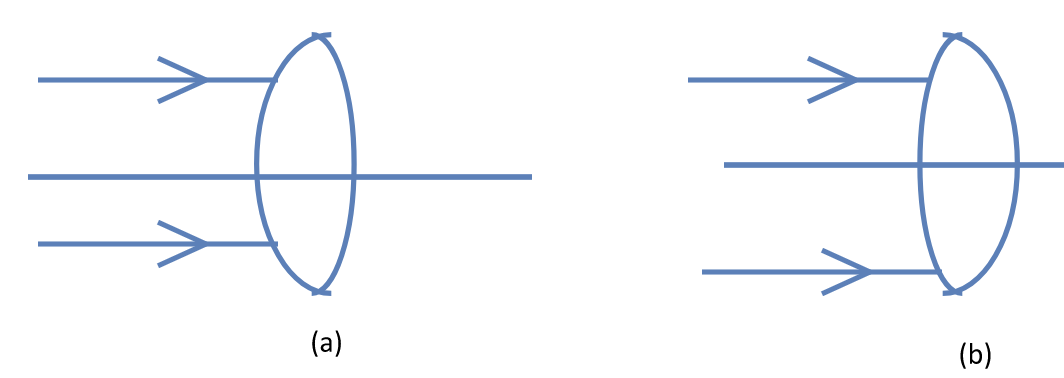
- The two surfaces of a convex lens have different radii (see figure). A parallel beam of light falls on the lens in two situations as shown in the figure. The image is formed at a distance $v_1$ in case (a) and at a distance $v_2$ in case (b). Should $v_1$ be smaller than, equal to, or greater than $v_2$?