Total Internal Reflection

Consider a light ray traveling from a denser medium (of refractive index $\mu_1$) to a rarer medium (of refractive index $\mu_2\,( < \mu_1)$ ). The ray gets reflected back if its angle of incidence $i$ is greater than the critical angle $i_c$ given by \begin{align} \theta_c=\sin^{-1}\left(\frac{\mu_2}{\mu_1}\right). \end{align} This phenomenon is called total internal reflection.

Demo using a dettol bottle

When light goes from a denser medium to a rarer medium, and the angle of incidence is larger than a critical value, called critical angle, whole of the light will get reflected at the surface. If the angle of incidence is smaller than the critical angle, part of the light is reflected and part of it is refracted. In this inexpensive demo we show the light paths as the medium changes and hence all phenomena on refraction can be visually seen. It is very simple and has been widely appreciated.

You need a Dettol bottle, some common salt, and a laser torch for this demo.

Take a dettol bottle and fill water in it up to say 3/4 of its height. Put some common salt in it. Tighten the cap. Put on a laser torch and send light from outside into the water obliquely. The front end of the torch should be in contact with the thinner side of the bottle at a height covered by water, and the incline of the torch should be adjusted by tilting the torch with your hand. Adjust the orientation so that the light goes parallel to the flat faces of the bottle, but at an angle to the surface of the water.

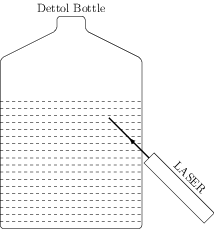
You should be able to see the path of the laser beam in the water. If it is not clearly visible, invert the bottle for a second. This will bring the salt sitting at the bottom in the whole water and make the path visible. Slowly change the orientation of the laser torch and you very clearly see the total internal reflection. If you make the torch closer to vertical, thus decreasing the angle of incidence, the reflected beam will loose its intensity. A spot will form on the opposite wall of the bottle above the water surface. This tells that a part of the beam is getting transmitted.

Now you put smoke of an incense stick into the bottle. It will collect above the water surface. Now when you send laser beam and if it gets transmitted to air side the transmitted beam will also be clearly seen, though it will be hazy. So for angles less than the critical angle you see both reflected and transmitted beams, and for angles larger than the critical angle, only reflected beam is observed.

Dettol bottle suites this demo because the walls are flat. This demo can be extended to informal lab, by encouraging students to adjust the torch for grazing angle refraction and measuring the inclination angle from vertical which is also the normal to the surface. This angle is the critical angle.

Optical fiber demo using water bottle

Optical fibres are long synthetic fibres used to transmit light from one place to another. They form the backbone of modern communication systems. They work on the principle of total internal reflection.

Make a hole near the bottom of the bottle/cup. Add little soap in the water and fill the bottle with this water. Point the laser beam at the hole in horizontal orientation. The light travels along the water stream. Put a finger in the water stream and see a spot of light on your finger.

In the water stream, light strike the interface between water and outside air at an angle more than the critical angle. So it is reflected back into the stream. This reflected beam too strike the opposite surface at an angle more than the critical angle and is again reflected back. This process goes on and on i.e., multiple total internal reflections takes place.

Problems from IIT JEE

Problem (IIT JEE 2014): A point source S is placed at the bottom of a transparent block of height 10 m and refractive index 2.72. It is immersed in a lower refractive index liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter 11.54 mm on the top of the block. The refractive index of the liquid is,

1. 1.21
2. 1.30
3. 1.36
4. 1.42

Solution: The rays stop coming to liquid side if the angle of incidence at the block-liquid interface is greater than the critical angle $\theta_c$ (see figure).

Let $\mu_b=2.72$ be the refractive index of the block and $\mu_l$ be the refractive index of the liquid. The critical angle is given by, \begin{align} \sin\theta_c=\frac{\mu_l}{\mu_b}. \end{align} From geometry, \begin{align} \sin\theta_c=\frac{r}{\sqrt{r^2+h^2}}. \end{align} Solve above equations to get, \begin{align} \mu_l &=\frac{\mu_b r}{\sqrt{r^2+h^2}} \\ &=\frac{2.72(11.54/2)}{\sqrt{(11.54/2)^2+10^2}} \\ &=1.36.\nonumber \end{align}

Related

1. Verification of Laws of Reflection
2. Refraction at Plane and Spherical Surfaces