Carnot Engine and Carnot Cycle

Carnot engine is a reversible engine of maximum efficiency. It operates between a hot reservoir at temperature T₁ and a cold reservoir at temperature T₂.

A Carnot cycle consists of following four processes

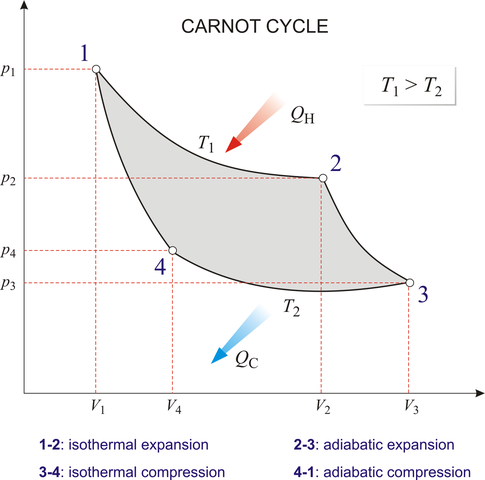
1. Isothermal expansion: $(p_1,V_1,T_1)\to (p_2, V_2, T_1)$. The heat absorbed in this process is $Q_1$ and work done by the gas is \begin{align} W_{1\to2}=nRT_1 \ln(V_2/V_1) \end{align}
2. Adiabatic expansion: $(p_2,V_2,T_1)\to(p_3,V_3,T_2)$. The work done by the gas is \begin{align} W_{2\to3}=nR(p_2V_2-p_3V_3)/(\gamma-1) \end{align}
3. Isothermal contraction: $(p_3,V_3,T_2)\to (p_4, V_4, T_2)$. The heat released in this process is $Q_2$ and work done by the gas is \begin{align} W_{3\to4}=nRT_2 \ln(V_4/V_3) \end{align}
4. Adiabatic contraction: $(p_4,V_4,T_2)\to(p_1,V_1,T_1)$. The work done by the gas is \begin{align} W_{4\to1}=nR(p_4V_4-p_1V_1)/(\gamma-1) \end{align}

The total work done by the gas in a cycle is $W$. The efficiency of the Carnot engine is given by \begin{align} \eta &=\frac{W}{Q_1} =1-\frac{Q_2}{Q_1} =1-\frac{T_2}{T1}. \end{align}

Note that $Q_2/Q_1=T_2/T_1$.

I encorage you to draw Carnot cycle on T-S (temperature-entropy) diagram.

Solved Problems from IIT JEE

Problem from IIT JEE 2018

One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where $V$ is the volume and $T$ is the temperature). Which of the statements below is (are) true?

1. Proecess I is an isochoric process.
2. In process II, gas absorbs heat.
3. In process IV, gas releases heat.
4. Process I and III are not isobaric.

Solution: The volume is constant in an isochoric process. It is parallel to $T$ axis on a $T\text{-}V$ diagram.

The process II is isothermal expansion as temperature is constant and volume is increased. The change in internal energy of a gas in an isothermal process is zero i.e., $\Delta U=0$. The work done by the gas in an expansion process is positive i.e., $\Delta W=\int p \mathrm{d}V > 0$. By first law of thermodynamics, $\Delta Q=\Delta U+\Delta W=\Delta W > 0$, i.e., heat is absorbed by the gas.

The process IV is isothermal compression as temperature is constant and volume is decreased. Thus, $\Delta U=0$, $\Delta W<0$ and $\Delta Q=\Delta W<0$ i.e., heat is released by the gas.

The pressure is constant in an isobaric process. It is a straight line, $T=(p/nR)V$, on a $T\text{-}V$ diagram. Can you relate the given cycle with Carnot cycle?

Questions on Carnot Engine

Question 1: The free expansion of a gas is an irreversible process.

A. True
B. False

Question 2: Which of the following statement is FALSE about a Carnot engine?

A. It is the only reversible engine possible that works between two reservoirs at different temperatures.
B. Its efficiency is more than any other engine operating between the same temperatures.
C. Its efficiency depends on the working substance.
D. The total entropy change in a Carnot cycle is zero.

Exercise

1. A heat engine operates in a Carnot cycle. Mark True/False
1. Throughout the operation the gas does positive work
2. Throughout the operation the gas absorbs heat
3. Throughout the operation the internal energy of the gas remains the same
4. In integral number of cycles the gas does positive work
5. In integral number of cycles the gas absorbs heat
6. In integral number of cycles, the internal energy of the system remains the same.

Related

1. Heat engine and refrigerator
2. First law of thermodynamics and its applications