Melde's experiment

Melde's experiment is used to study standing waves on a string. It consists of a light string tied to one of the prongs of a tuning fork. The other end of the string is pased over a horizontal pulley and a pan is suspended from the free end. The tension of the string can be adjusted by changing the weights placed in the pan. The length of the string can be adjusted by changing the position of the pulley towards or away from the fork. The numbers of loops formed in the strin can be varied by adjusting the length of the string or the tensionin the string.

Melde's experiment in longitudinal mode

In longitudinal mode, the string is tied to one arm of the tuning fork such that longitudinal waves are formed in the string. In longitudinal mode, the frequency of the fork ($\nu_f$) is twice the frequency of the string ($\nu_s$). If there are $p$ loops in the string then its frequency is \begin{align} \nu_s=\frac{p}{2l}\sqrt{\frac{T}{\mu}} \end{align} The condition $\nu_f=2\nu_s$ gives \begin{align} \nu_f=\frac{p}{l}\sqrt{\frac{T}{\mu}} \end{align}

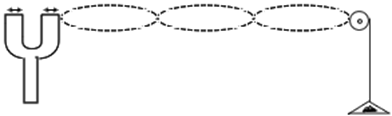
Melde's experiment in transverse mode

In transverse mode, the string is tied to one arm of the tuning fork such that transverse waves are formed in the string. In transverse mode, the frequency of the fork ($\nu_f$) and the frequency of the string ($\nu_s$) are equal. If there are $p$ loops in the string then its frequency is \begin{align} \nu_s=\frac{p}{2l}\sqrt{\frac{T}{\mu}} \end{align} The condition $\nu_f=\nu_s$ gives \begin{align} \nu_f=\frac{p}{2l}\sqrt{\frac{T}{\mu}} \end{align}

Related video

Related

1. Waves on a string

Subscribe to our channel