Physical Pendulum

A physical pendulum is a rigid body pivoted at the point O. When displaced slightly, it executes angular simple harmonic motion in the vertical plane with a time period \begin{align} T=2\pi\sqrt{\frac{I}{mgl}}\nonumber \end{align} where $I$ is the moment of inertia about the axis of rotation passing through the point of suspension O and $l$ is the distance of the centre of mass C from the point O.

The restoring torque on the physical pendulum about the point O is $\tau=mg l\sin\theta $. The pendulum rotates about a fixed axis through O. The relation $\tau=I\alpha$ gives equation of motion of the physical pendulum \begin{align} \frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}=-\frac{mgl\sin\theta}{I}\approx-\frac{mgl}{I}\theta \nonumber \end{align} This is the differential equation for angular SHM. Its solution with initial condition $\theta=\theta_0$ and $\dot\theta=0$ (pendulum released from initial angle $\theta_0$) is \begin{align} \theta=\theta_0 \cos(\omega t) \end{align} A physical pendulum can be used to measure acceleration due to gravity $g$ (similar to simple pendulum). The physical pendulum is also used to measure the moment of inertia of a body.

Equivalent simple pendulum

Let $k$ be the radius of gyration of the body. The moment of inertia about the parallel axis through the centre of mass C is $I_C=mk^2$. The moment of inertia about an axis through suspension point is \begin{align} I=mk^2+ml^2. \end{align}

The time period of the physical pendulum, \begin{align} T&=2\pi\sqrt{\frac{m(k^2+l^2)}{mgl}} \\ &=2\pi \sqrt{\frac{k^2/l+l}{g}} \end{align} is same as time period of simple pendulum of length $l_s=l+k^2/l$. The simple pendulum of length $l_s=l+k^2/l$ is called equivalent simple pendulum.

Length for minimum time period

The time period of a physical pendulum varies with $l$. The time period is minimum if $l=k$. The length of equivalent simple pendulum is $l_s=2k$. The time period is infinite if $l=0$.

If we suspend a physical pendulum from a point G located on extension of line OC at a distance $l^2/k$ from C then its time period remains same. The point O and G are equivalent.

There are four suspension points (two towards O and another two towards G) that gives same time period. We encourage you to find distances of these four points (from C) in terms of $T$. Plot $l\text{-}T$ graph for the physical pendulum.

Experiment to determine moment of inertia

The oscillations of a physical pendulum can be used to find moment of inertia of a body. The time period of a physical pendulum varies with its length as \begin{align} T=2\pi \sqrt{\frac{k^2/l+l}{g}}. \end{align} Square and simplify to get \begin{align} \frac{g}{4\pi^2} (lT^2)=l^2+k^2 \end{align} The graph between $l^2$ and $lT^2$ is a straight line. The intercept on the $l^2$ axis gives $k^2$. The moment of inertia about the axis passing through the centre of mass is $I_C=mk^2$.

In the experiment, $l$ is varied and corresponding $T$ is measured. Then $l^2$ versus $lT^2$ graph is plotted to get the radius of gyration.

One such experiment is: To determine, by the method of oscillations, the moment of inertia of a rectangular lamina about an axis perpendicular to its plane passing through its centre. You need a rectangular lamina with several holes, a horizontal knife edge attached to rigid support, a plumb line, a stop-watch and a meter scale for this experiment.

Solved Problems on Physical Pendulum

Problem from IIT JEE 2011

A metal rod of length $L$ and mass $m$ is pivoted at one end. A thin disc of mass $M$ and radius $ R( < L ) $ is attached at its centre to the free end of rod. Consider the two ways the disc is attached. (Case A) The disc is not free to rotate about its centre, and (Case B) the disc is free to rotate about its centre. The rod-disc system performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is (are) true?

1. restoring torque in case A = restoring torque in case B.
2. restoring torque in case A $<$ restoring torque in case B.
3. Angular frequency of case A $>$ Angular frequency of case B.
4. Angular frequency of case A $<$ Angular frequency of case B.

Solution: Consider motion of the centre of mass C located at a distance $r_C=\frac{M+m/2}{M+m}\,L$ from the pivot point O.

The weight of disc-rod system, $(M+m)g$, acts at C giving an anticlockwise restoring torque about O, \begin{align} \tau&=(M+m)gr_C \sin\theta\nonumber\\ &=\left(M+m/2\right)gL\sin\theta,\nonumber \end{align} where $\theta$ is angular displacement. Since forces remain the same, restoring torques are equal in both, case A and case B. Since system is released from the same position, initial potential energy of the system is equal in both the cases i.e., $U_{A}^{i}=U_{B}^{i}$. Initial kinetic energy is zero in both the cases i.e., $K_{A}^{i}=K_{B}^{i}=0$. The potential energy at the lowest point is also zero i.e., $U_{A}^{f}=U_{B}^{f}=0$. The energy conservation, $U_{A}^{i}+K_{A}^{i}=U_{A}^{f}+K_{A}^{f}$ and $U_{B}^{i}+K_{B}^{i}=U_{B}^{f}+K_{B}^{f}$, gives $K_{A}^f=K_{B}^f$. In Case A, the disc is rigidly fixed to the rod and the disc-rod system has pure rotational motion about an axis passing through O. Thus, \begin{align} K_{A}^{f}&=\tfrac{1}{2}I_{O}\omega_{A}^2 \nonumber\\ &=\tfrac{1}{2}\left(\tfrac{1}{3}mL^2+\tfrac{1}{2}MR^2+ML^2\right)\omega_{A}^2 \nonumber\\ &=\left(\tfrac{1}{6}mL^2+\tfrac{1}{2}ML^2+\tfrac{1}{4}MR^2\right)\omega_{A}^2.\nonumber \end{align} In Case B, the rod undergoes pure rotation about O and the disc has both translation and rotation. The kinetic energy of the rod is \begin{align} K_\text{B,rod}^{f}&=\tfrac{1}{2}I_\text{O,rod}\,\omega_{B}^2 \nonumber\\ &=\tfrac{1}{2}\tfrac{1}{3}mL^2\omega_{B}^2=\tfrac{1}{6}mL^2\omega_{B}^2, \nonumber \end{align} and the kinetic energy of the disc is \begin{align} K_\text{B,disc}^f&=\tfrac{1}{2}Mv_{cm}^2+\tfrac{1}{2}I_{cm}\omega^2 \nonumber\\ &=\tfrac{1}{2}M(L\omega_B)^2+\tfrac{1}{2}\tfrac{1}{2}MR^2\omega^2\nonumber\\ &=\tfrac{1}{2}ML^2\omega_{B}^2+\tfrac{1}{4}MR^2\omega^2, \nonumber \end{align} where $\omega$ is the angular velocity of the disc. Using, $K_{B}^f=K_\text{B,rod}^f+K_\text{B,disc}^f$ and equating $K_A^f$ to $K_B^f$, we get \begin{align} \label{eqn:kaa:4} \omega_B^2=\omega_A^2+\frac{3}{2}\cdot\frac{MR^2}{mL^2+3MR^2}\left(\omega_A^2-\omega^2\right). \end{align} Now, consider the motion of the disc alone. When released, the disc was at rest with its angular velocity $\omega=0$ and the angular momentum about its centre of mass $L=I_\text{cm}\omega=0$. There is no external torque on the disc about its centre of mass because the disc is free to rotate and its weight pass through the centre of mass. Thus, angular momentum of the disc about its centre of mass is conserved i.e., angular momentum and angular velocity of the disc always remains zero. Substitute $\omega=0$ in above equation to get $\omega_B>\omega_A$.

Problem to find Suspension Point that Minimizes the Time Period

A thin disc of radius $r$ and mass $m$ is suspended as a pendulum in a vertical plane from a point O located at a distance $x$ above its center. It undergoes small angular oscillations. For what value of $x$, the amplitude of angular acceleration of the disc is minimum?

1. $r/\sqrt{2}$
2. $r/\sqrt{3}$
3. $r$
4. $\sqrt{3}r/2$

Solution: Consider a time instant when angular displacement of the disc is $\theta$ (see figure). The forces acting on the disc are its weight $mg$ at its centre of mass C and the reaction $R$ at the pivot point O.

Resolve $mg$ along and perpendicular to OC. The torque on the disc about the fixed point O is given by \begin{align} \tau_O=mg x \sin\theta,\quad\text{(clockwise)}.\nonumber \end{align} The angular acceleration of the disc is given by \begin{align} \alpha=\frac{\tau_O}{I_O}=\frac{mgx \sin\theta}{mr^2/2+mx^2}=\frac{2gx}{r^2+2x^2}\sin\theta,\nonumber \end{align} where we used parallel axis theorem to get moment of inertia of the disc about the horizontal axis passing through O. Note that $\theta$ varies with time. The amplitude of the angular acceleration of the disc is \begin{align} \alpha_0=\frac{2gx}{r^2+2x^2}.\nonumber \end{align} Differentiate $\alpha_0$ with $x$ and equate the derivative to zero to get $x$ at which $\alpha_0$ attain its maximum i.e., \begin{align} \frac{\mathrm{d}\alpha_0}{\mathrm{d}x}=\frac{2gx(4x)-2g(r^2+2x^2)}{(r^2+2x^2)^2}=0,\nonumber \end{align} which gives $x=r/\sqrt{2}$. We encourage you to show that the disc undergoes SHM. The frequency of oscillations is maximum at $x=r/\sqrt{2}$.

Problem on Centre of Percussion and Kater's Pendulum

A rigid body can rotate about a fixed point O as shown in the figure. The moment of inertia of the body about the point O is $I_0$ and the distance between O and the centre of mass C of the body is $d$. A force $F$ is applied to the body perpendicular to the line joining O and the centre of mass, at a distance $x$ from O. Find the distance $x$ for which there will be no reaction at the point O in the direction of F. Neglect gravity.

1. $d$
2. $2I_O/(md)$
3. $d/2$
4. $I_O/(md)$

Solution: Let reaction force at the pivot point O is zero. The torque about the fixed point O is $\tau_O=xF$ (counter clock wise). Use $\tau_O=I_O\alpha$ to get the angular acceleration of the body \begin{align} \label{ahd:eqn:1} \alpha=xF/I_O. \end{align} The torque about the centre of mass C is $\tau_C=(x-d)F$. Use $\tau_C=I_C\alpha$ to get \begin{align} \label{ahd:eqn:2} \alpha=\frac{(x-d)F}{I_C}=\frac{(x-d)F}{I_O-md^2}, \end{align} where we used parallel axis theorem, $I_O=I_C+md^2$, to get moment of inertia of the body about an axis passing through the centre of mass C. Eliminate $\alpha$ from above equations to get $x=I_O/(md)$.

The point P is called centre of percussion of the body. If line of action of the force $F$ is perpendicular to OC and passes through P then reaction force at the point O is zero. Let us see some real life situations where centre of percussion plays an important role.

In the game of cricket, if you hold the bat at O and the ball hits at the centre of percussion P then you feel comfortable because reaction force at your hands is zero. If the ball hits at some other point than you feel JhanJhanaHat (stinging) in your hands.

Another situation is Kater's reversible pendulum. The body oscillate under the action of gravity if it is suspended from a point. The oscillation frequency is same whether you suspend the body from the point O or from the point P.

Experiment to determine $g$ with a Kater's Pendulum

Kater's pendulum consists of a non-uniform metal rod such that its centre of mass is close to one end than the other end. It has two knife edges $K_1$ and $K_2$ and adjustable weights. The weights are used to make the period about the two knife edges the same.

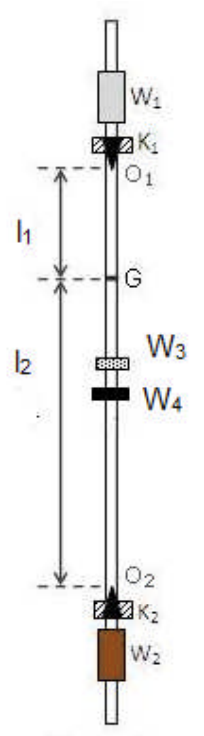
If two points collinear with the centre of mass and on opposite sides of it are found about which the periods of the pendulum are equal, the distance between them will be equal to the length of the equivalent simple pendulum, and can be used for the accurate determination of $g$ i.e., \begin{align} T_1=T_2=T=2\pi\sqrt{\frac{l_1+l_2}{g}}. \end{align}

The time period $T_1$ and $T_2$ are related to $l_1$ and $l_2$ by \begin{align} \frac{4\pi^2}{g}=\frac{T_1^2+T_2^2}{2(l_1+l_2)}+\frac{T_1^2-T_2^2}{2(l_1-l_2)} \end{align} If $T_1$ and $T_2$ are nearly equal and there is considerable difference between $l_1$ and $l_2$ i.e., centre of mass is not nearly midway between the knife edges (which is essential feature of a Kater's pendulum) then the second term will be very small compared with the first. Hence an approximate knowledge of $(l_1-l_2)$ will be sufficient to get $g$.

More Problems on Physical Pendulum

A Ring Hanging from a Peg

A physical pendulum consists of a ring of radius $R$ and mass $m$. The ring is pivoted at point on its perimeter. The ring is pulled out such that its center of mass makes a small angle $\theta_0$ from the vertical and released from rest.

1. What is the angular frequency of oscillation?
2. What is the angular speed of the ring at the bottom of its swing?

A Hanging Metre Stick

A physical pendulum consists of a meter stick that is pivoted at a small hole drilled through the stick at a distance $d$ from the 50 cm mark. The period of oscillation is 2.5 s. Find $d$.

Disc Attached to a Light Rod

A physical pendulum consists of a disc of mass $m=1$ kg and radius $R=5$ cm fixed at the end of a massless rod. The other end of the rod is pivoted about point P on the ceiling. The distance from the pivot point to the center of mass of the bob is $l=4$ m. Initially the bob is released from rest from a small angle $\theta_0$ with respect to the vertical. Find the period of the bob?

Questions on Physical Pendulum

Question 1: In an experiment to measure the acceleration due to gravity, a metre stick of mass $m$ and length $L$ was used as a physical pendulum. Multiple small holes are drilled in the metre stick to suspend it from different points. A student measured the time period $T$ for different $l$ (by suspending metre stick from different holes). Which of the following statement is correct

A. The graph between $T^2l$ and $l^2$ is a straight line.
B. The graph between $T^2$ and $1/l$ is a straight line.
C. The graph between $T^2$ and $l$ is a rectangular hyperbola.
D. The graph between $T^2$ and $1/l$ is a rectangular hyperbola.

Question 2: Three physical pendulums A, B, and C, of masses $m_0 $, $2m_0$ and $3 m_0$ respectively, have the same shape and the same dimensions. Which of the following is correct

A. The time period of A is maximum
B. The time period of B is maximum
C. The time period of C is maximum
D. All have the same time period

Question 3: Three physical pendulums consisting of identical uniform spheres of the same mass $m$ that are rigidly connected by identical rods of length $l$ and negligible mass. Each pendulum is vertical and can pivot about suspension point P. The increasing order of their time periods is?

A. (iii), (i), (ii).
B. (ii), (i), (iii).
C. (i), (iii), (ii).
D. (ii), (iii), (i).

Related

1. Torsional pendulum
2. Simple Harmonic Motion
3. Dynamics of rigid bodies with fixed axis of rotation

References

1. 300 Solved Problems on Rotational Mechanics by Jitender Singh and Shraddhesh Chaturvedi
2. Concepts of Physics Part 1 by HC Verma (Link to Amazon)
3. Physical pendulum experiments to enhance the understanding of moments of inertia and simple harmonic motion (paper, pdf)
4. Physical Pendulums and Small Oscillations (MIT, pdf)