Sound waves in a pipe
The particle's displacement in a sound wave is given by (displacement wave) \begin{align} s=s_0\sin \omega(t-x/v) \end{align}
The pressure in a sound wave is given by (pressure wave) \begin{align} p=p_0\cos \omega(t-x/v),\; p_0=(B\omega/v)s_0. \end{align} Note the phase difference between displacement wave and pressure wave.
The speed of sound waves in liquid, solid, and gases are given by \begin{align} v_\text{liquid} & = \sqrt{\frac{B}{\rho}} \\ v_\text{solid} & =\sqrt{\frac{Y}{\rho}} \\ v_\text{gas} & =\sqrt{\frac{\gamma P}{\rho}} \end{align}
The intensity of sound wave is given by \begin{align} I & =\frac{2\pi^2B}{v}{s_0}^2\nu^2 \\ & =\frac{{p_0}^2 v}{2B} \\ &=\frac{{p_0}^2}{2\rho v} \end{align}
The standing longitudinal waves are \begin{align} p_1 & =p_0\sin \omega(t-x/v) \\ p_2 & =p_0\sin\omega(t+x/v) \\ p &=p_1+p_2=2p_0\cos kx \sin \omega t \end{align}
Sound waves in a pipe closed at one end (closed organ pipe)
The particle's displacement is zero at the closed end and it is maximum at the open end. This is given by the boundary condition: $y=0$ at $x=0$. The allowed frequencies in an organ pipe closed at one end are: \begin{align} L & =\left(2n+1\right)\frac{\lambda}{4} \\ \nu & =(2n+1)\frac{v}{4L} \\ n & =0,1,2,\ldots \end{align}
The frequency of fundamental or 1st harmonics is given by \begin{align} \nu_0=\frac{v}{4L} \end{align}
First overtone or 3rd harmonics is given by \begin{align} \nu_1=3\nu_0=\frac{3v}{4L} \end{align}
Second overtone or 5th harmonics is given by \begin{align} \nu_2=5\nu_0=\frac{5v}{4L} \end{align}
Only odd harmonics are present in an organ pipe closed at one end.
Sound waves in a pipe open at both ends (open organ pipe)
The particle's displacement is maximum at the both ends. The allowed frequencies in an open organ pipe are: \begin{align} L & =n\frac{\lambda}{2},\\ \nu &=n\frac{v}{4L},\\ n&=1,2,\ldots \end{align}
The frequency of fundamental or 1st harmonics is given by \begin{align} \nu_0=\frac{v}{2L} \end{align}
First overtone or 2nd harmonics is given by \begin{align} \nu_1=2\nu_0=\frac{2v}{2L} \end{align}
Second overtone or 3rd harmonics is given by \begin{align} \nu_2=3\nu_0=\frac{3v}{2L} \end{align}
All harmonics are present in an open organ pipe.
Problems from IIT JEE
Problem (IIT JEE 2010): A hollow pipe of length 0.8 m is closed at one end. At its open end a 0.5 m long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the string is 50 N and the speed of sound is 320 m/s, the mass of the string is,
- 5 grams
- 10 grams
- 20 grams
- 40 grams
Solution: The fundamental mode in a pipe closed at one end and the second harmonic in a string are shown in figure.
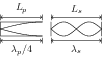
It can be seen that $\lambda_p/4=L_p$ and $\lambda_s=L_s$. For the pipe closed at one end, \begin{align} \nu_p &=\frac{v_p}{\lambda_p} \\ &=\frac{v_p}{4L_p} \\ &=\frac{320}{4(0.8)}=100\;\mathrm{Hz}, \end{align} where $v_p={320}\;\mathrm{m/s}$ is the velocity of sound in the pipe and $L_p={0.8}\;\mathrm{m}$ is length of the pipe. For string of mass $m$, length $L_s$ and having tension $T$, velocity of sound in the string is given by, \begin{align} \nu_s &=\frac{v_s}{\lambda_s} \\ &=\frac{\sqrt{T/(m/L_s)}}{L_s} \\ &=\sqrt{\frac{T}{mL_s}} \\ &=\sqrt{\frac{50}{m(0.5)}}=\frac{10}{\sqrt{m}}. \end{align} At resonance, $\nu_p=\nu_s$. Substitute $\nu_p$ and $\nu_s$ from first and second equations to get $m={0.01}\;\mathrm{kg}={10}\;\mathrm{gram}$.
