Capacitors in Series and Parallel
The equivalent capacitance $C_s$ of two capacitors $C_1$ and $C_2$ connected in series is given by \begin{align} \frac{1}{C_s}=\frac{1}{C_1}+\frac{1}{C_2}. \end{align}
The equivalent resistance $C_p$ of two capacitors $C_1$ and $C_2$ connected in parallel is given by \begin{align} C_p=C_1+C_2 \end{align}
The above formulas can be generalized for three or more capacitors.
Problems from IIT JEE
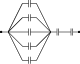
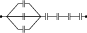
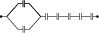
Problem (IIT JEE 1990): Seven capacitors each of capacitance ${2}\;\mathrm{\mu F}$ are connected in a configuration to obtain an effective capacitance ${\frac{10}{11}}\;\mathrm{\mu F}$. Which of the following combination will achieve the desired result?
Solution: In option A, equivalent capacitance of five capacitors in parallel is $C_1={10}\;\mathrm{\mu F}$ and that of two capacitors in series is $C_2={1}\;\mathrm{\mu F}$. The $C_1$ and $C_2$ in series give equivalent capacitance $C_\text{eq}=\frac{C_1C_2}{C_1+C_2}={\frac{10}{11}}\;\mathrm{\mu F}$.
Exercise
- A finite ladder is constructed by connecting several sections of $2\mu F, 4\mu F$ capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance $C$. What value should be chosen for $C$, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between?