Energy Stored in Capacitor
Let a parallel plate capacitor of capacitance $C$ has a charge $Q$ ($+Q$ on one plate and $-Q$ on another). The potential difference between its plate is given by \begin{align} V=\frac{Q}{C}. \end{align}
The electrostatic energy stored in the capacitor is given by \begin{align} U &=\frac{1}{2}CV^2 \\ &=\frac{Q^2}{2C} \\ &=\frac{1}{2}QV. \end{align}
The energy $U$ of an electrostatic field $E$ per unit volume $V$ is given by \begin{align} \frac{U}{V}=\frac{1}{2}\epsilon_0 E^2. \end{align}
Problems from IIT JEE
Problem (IIT JEE 2002): Two identical capacitors have the same capacitance $C$. One of them is charged to potential $V_1$ and the other to $V_2$. The negative ends of the capacitors are connected together. When the positive ends are also connected, the decrease in energy of the combined system is,
- $\frac{1}{4}C\left(V_{1}^{2}-V_{2}^{2}\right)$
- $\frac{1}{4}C\left(V_{1}^{2}+V_{2}^{2}\right)$
- $\frac{1}{4}C\left(V_{1}-V_{2}\right)^2$
- $\frac{1}{4}C\left(V_{1}+V_{2}\right)^2$
Solution: Initially, total electrostatic energy stored in two capacitors is $U_i=\frac{1}{2}CV_1^2+\frac{1}{2}CV_2^2$.
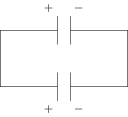
Initial charges on two capacitors are $q_1=CV_1$ and $q_2=CV_2$. Let $q_1^\prime$ and $q_2^\prime$ be charges on capacitors when same terminals of two capacitors are connected to each other (see figure). By charge conservation, \begin{align} q_1^\prime+q_2^\prime=q_1+q_2. \end{align} The potential $V^\prime$ across two capacitors is equal, i.e., \begin{align} &q_1^\prime /C=q_2^\prime /C. \end{align} Solve above equations to get, \begin{align} q_1^\prime & =q_2^\prime \\ &=(q_1+q_2)/2, \text{and} \\ V^\prime &=(V_1+V_2)/2. \nonumber \end{align} Thus, final electrostatic energy stored in the two capacitors is, \begin{align} U_f &=\tfrac{1}{2}CV^2+\tfrac{1}{2}CV^2 \\ &=\tfrac{1}{4}C(V_1^2+V_2^2+2V_1V_2), \nonumber \end{align} and loss in energy is \begin{align} U_i-U_f=\frac{1}{4}C(V_1-V_2)^2. \end{align}
