Centre of Mass and its Motion
The centre of mass of an object is a point where its total mass can be assumed to be located for studying its translatory motion.
The centre of mass of a discrete mass distribution is given by \begin{align} x_\text{cm}=\frac{\sum x_im_i}{\sum m_i}. \end{align}
The centre of mass of a continuous mass distribution is given by \begin{align} x_\text{cm}=\frac{\int x\mathrm{d}m}{\int\mathrm{d}m}, \end{align}
Centre of mass of a few useful configurations
The centre of mass of two particles of masses $m_1$ and $m_2$ separated by a distance $r$ lies at a distance $\frac{m_2 r}{m_1+m_2}$ from $m_1$.
The centre of mass of a triangle lies at its centroid. The centre of mass of an equilateral triangle of height $h$ lies at a height $y_c=h/3$ from its base.
The centre of mass of a semicircular ring of radius $r$ lies at a distance $y_c=\frac{2r}{\pi}$ from its centre.
The centre of mass of a semicircular disc of radius $r$ lies at a distance $y_c=\frac{4r}{3\pi}$ from its centre.
The centre of mass of a hemispherical shell of radius $r$ lies at a distance $y_c=\frac{r}{2}$ from its centre.
The centre of mass of a hemisphere of radius $r$ lies at a distance $y_c=\frac{3r}{8}$ from its centre.
The centre of mass of a solid cone of height $h$ lies at a height $h/4$ from its base. The centre of mass of a hollow cone of height $h$ lies at a height $h/3$ from its base.
Motion of the Centre of Mass
The centre of mass moves with the object. The velocity of the centre of mass is given by \begin{align} \vec{v}_\text{cm}=\frac{\sum m_i \vec{v}_i }{M} \end{align} where $M=\sum m_i$. The linear momentum of the centre of mass is \begin{align} \vec{p}_\text{cm}=M\vec{v}_\text{cm}, \end{align} and its acceleration is given by \begin{align} \quad\vec{a}_\text{cm}=\frac{\vec{F}_\text{ext}}{M} \nonumber \end{align}
Worked out Problems
Problem: A composite body is formed by joining a solid cylinder and a solid cone of the same radius. The length of the cylinder is $b$ and height of the cone is $h$. If the centre of mass of the composite body is located in the plane between the solid cone and the solid cylinder then the ratio $b/h$ is
(A) $1/\sqrt{6}$ (B) $1/2$ (C) $1/\sqrt{5}$ (D) $1/3$
Solution: Let the origin be located at the plane between the solid cone and the solid cylinder. Let $x$ axis is along the symmetric axis towards the right.The centre of mass of the solid cylinder is at a distance $x_1=-b/2$. The centre of mass of the solid cone is at a distance $x_2=h/4 $ (at distance h/4 from the base).
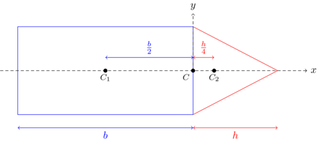
Let $\rho$ be the mass density and $r$ be the radius of the cylinder and the cone. The mass of the cylinder is $m_1=\rho (\pi r^2 b)$ and mass of the cone is $m_2=\rho (\frac{1}{3} \pi r^2 h)$. For the centre of mass of the composite body to be at origin, \begin{align} x_{cm} &=\frac{m_1x1+m_2 x_2}{m_1+m_2} \\ &=\frac{\rho (\pi r^2 b) (-b/2) + \rho (\frac{1}{3} \pi r^2 h) (h/4) }{\rho (\pi r^2 b)+ \rho (\frac{1}{3} \pi r^2 h)}\\ &=0. \nonumber \end{align} Simplify to get $b/h=1/\sqrt{6}$.
Problems from IIT JEE
Problem (IIT JEE 2009): Look at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is $m$. The mass of the ink used to draw the outer circle is $6m$. The coordinates of the centres of the different parts are: outer circle $(0,0)$, left inner circle $(-a,a)$, right inner circle $(a,a)$, vertical line $(0,0)$ and horizontal line $(0,-a)$. The $y$-coordinate of the centre of mass of the ink in this drawing is,
- $a/10$
- $a/8$
- $a/12$
- $a/3$
Solution: Due to uniform line thickness, the centre of mass of circle lies on its centre and that of a line segment lies in its middle. The $y$ coordinate of the centre of mass of the ink given in the drawing is given by, \begin{align} y_\text{cm} & =\frac{\sum m_iy_i}{\sum m_i} \\ &=\frac{6m(0)+m(a)+m(a)+m(0)+m(-a)}{6m+m+m+m+m} \\ &=\frac{a}{10}.\nonumber \end{align}
Problem (IIT JEE 2003): Two point masses $m_1$ and $m_2$ are connected by a spring of spring constant $k$ and natural length $l_0$. The spring is compressed such that the two point masses touch each other and then are fastened by a string. Then the system is moved with a velocity $v_0$ along positive $x$-axis. When the system reaches the origin the string breaks $(t=0)$. The position of the point mass $m_1$ is given by \begin{align} x_1=v_0 t-A(1-\cos\omega t), \end{align} where $A$ and $\omega$ are constants. Find the position of the second block as a function of time. Also find the relation between $A$ and $l_0$.
Solution: Consider $m_1$, $m_2$, and the spring together as a system. At $t=0$, the position and velocity of the centre of mass of the system are, \begin{align} \label{pqb:eqn:1} &x_\text{cm}=\frac{m_1x_1+m_2x_2}{m_1+m_2}=0,\\ \label{pqb:eqn:2} &v_\text{cm}=\frac{\mathrm{d}x_\text{cm}}{\mathrm{d}t}=\frac{m_1v_1+m_2v_2}{m_1+m_2}=v_0. \end{align} There is no external force on the system. Hence, $v_\text{cm}$ remains constant at $v_0$. Integrate above equation with the initial condition $x_\text{cm}=0$ at $t=0$ to get, \begin{align} \label{pqb:eqn:3} x_\text{cm}=\frac{m_1x_1+m_2x_2}{m_1+m_2}=v_0 t. \end{align} Given, the displacement of $m_1$ at time $t$ is, \begin{align} \label{pqb:eqn:4} x_1=v_0t-A(1-\cos\omega t). \end{align} Substitute $x_1$ from fourth equation into third equation to get the displacement of $m_2$ as, \begin{align} \label{pqb:eqn:5} x_2=v_0t+\frac{m_1}{m_2}A(1-\cos\omega t). \end{align} The forces on $m_1$ and $m_2$ become zero whenever the distance between the two particles is equal to the natural length of the spring i.e., \begin{align} \label{pqb:eqn:6} x_2-x_1 &=A\left(\frac{m_1}{m_2}+1\right)(1-\cos\omega t) \\ &=l_0. \end{align} Newton's second law gives force on $m_1$ as, \begin{align} m_1\frac{\mathrm{d}^2x_1}{\mathrm{d}t^2}=-A\omega^2\cos\omega t, \end{align} which becomes zero whenever $\cos\omega t=0$. Substitute $\cos\omega t=0$ in above equation to get $l_0=\left(m_1/m_2+1\right)A$.
Related
Subscribe to our channel
