Water Bottle in Free Fall
The concept of weight and weightlessness is often not easy. We define weight \(W\) of a body as the gravitational force that the earth exerts on the body. However, it is measured by measuring the effect of some kind of contact force. When we stand on a weighing machine, our legs press the machine downward and it is this contact force \(F\) that causes compression in the spring inside the balance. The compression in the spring is displayed as a weight. The connecting link is Newton's first and third laws. As the body pushes the machine down by a force \(F\), the machine pushes it up by the same force. As the body is in equilibrium, \(F=W\).
If the weighing machine (together with the body on it) is in free fall, the contact force \(F\) becomes zero. This is expressed by saying that the body has become weightless. If you use a freely falling frame, all phenomenon can be described by assuming \(g=0\) and then applying Newton's laws.
Procedure
Take a bottle of 1 litre capacity. Make a small hole in its wall near the bottom. Put a piece of empty pen refill in the hole. Hold the bottle in your hand, close the hole by a finger and fill water in it. Remove the finger and see that water comes out of the hole and goes in a parabolic path. Now leave the bottle from a height and catch it before it falls on the floor. As long as it is falling, there will not be any parabolic stream. Once you catch it, the stream will reappear.
Discussion
During the free fall, the water in the bottle is in state of weightlessness and does not push through the hole.
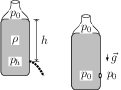
Weightlessness shows up in this demo through the vanishing of pressure difference between the water at top surface and just inside the hole. When the bottle is stationary, this pressure at the hole is \(p_h=p_0+h\rho g\), where \(p_0\) is pressure at the surface (atmospheric pressure), \(h\) is the height of the water column and \(\rho\) is the density of water. When in free fall, in the frame attached to the bottle we can substitute \(g=0\) and the pressure just inside the hole become \(p_h=p_0\). The pressure outside the hole is also equal to \(p_0\). Thus there is no pressure difference for the water to flow out of the hole.
Related
Subscribe to our channel
