Wien's Displacement Law

By Jitender Singh on Nov 5, 2019

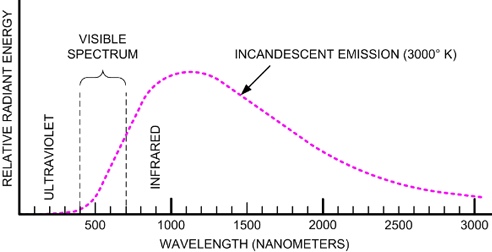
A blackbody emits radiation of all wavelengths. A plot of the intensity of emitted radiation (energy per unit area per unit time) for various wavelengths is called the blackbody spectrum. The intensity of emitted radiation in a wavelength range $(\lambda,\lambda+\mathrm{d}\lambda)$ increases with the increase in temperature for all wavelengths. However, at a given temperature $T$, the intensity is low for small wavelength, increases to a maximum value at a wavelength $\lambda_\mathrm{max}$, and then decreases as wavelength increases further.

Blackbody Spectrum — Blackbody spectrum at two different temperatures $T_1$ and $T_2$. The intensity attains maximum at wavelength given by Wien's displacement law $\lambda_\mathrm{max}T=b$.

According to Wien’s displacement law, the wavelength at which the intensity of radiation is maximum $(\lambda_\mathrm{max})$ for a blackbody radiating at absolute temperature $T$ is given by, \begin{align} \lambda_\mathrm{max} T=b=2.9\times 10^{-3}\; \mathrm{m\, K},\nonumber \end{align} where $\lambda_\mathrm{max}$ is wavelength in metre, $T$ is temperature in Kelvin and $b=2.9\times 10^{-3}\; \mathrm{m\, K}$ is Wien’s displacement constant. Note that the temperature of a body emitting radiation of blue color (maximum intensity at a wavelength of blue color) is more than the temperature of a body emitting radiation of red color (maximum intensity at a wavelength of red color).

Wien's law was based on the experimental results. It can be derived from Planck’s law ³. It may be noted that intensity is not maximum⁴ at the frequency $c/\lambda_\mathrm{max}$.

Interesting Problems on Wien's Displacement Law

Problem 1: Temperature of the Sun Surface

The wavelength of maximum solar emission is observed to be approximately $0.475\,\mathrm{\mu m}$. What is the surface temperature of the sun (assumed as blackbody)?

Solution: Given $\lambda_\mathrm{max}=4.75\times10^{-7}$ m. Apply Wien's displacement law to get surface temperature of the sun $ T=b/\lambda_\mathrm{max}=6100 \mathrm{K}$.

Problem 2: Infrared Radiations from the Human Body

The temperature of the human body is 37 deg C. The intensity of radiation emitted by the human body is maximum at a wavelength?

Solution: Given $T=37+273=310\,\mathrm{K}$. Apply Wien's displacement law to get the wavelength at which emitted radiation have maximum intensity $\lambda_\mathrm{max}=b/T=9.4\times10^{-6} \mathrm{m}$. This wavelength lies in the infrared region.

The temperature of the earth surface is close to 300 K. Thus, radiations emitted by the earth surface are mostly infrared. These infrared radiations cannot pass through the atmosphere. This is one of the reason for global warming (Greenhouse effect).

Problem 3: Cosmic Microwave Background Radiations

The Cosmic Microwave Background radiation (CMB) fills the universe. If temperature of the space is 2.7 K then CMB attains intensity maxima at a wavelength?

Solution: Given $T=2.7\,\mathrm{K}$. Apply Wien's displacement law to get the wavelength at which emitted radiation have maximum intensity $\lambda_\mathrm{max}=b/T\approx 10^{-3} \mathrm{m}=1\,\mathrm{mm}$. This wavelength lies in the microwave region.

Solved Problems from IIT JEE

Problem from IIT JEE 2005

Variation of radiant energy emitted by the sun, filament of tungsten lamp, and welding arc as a function of its wavelength is shown in figure. Which of the following option gives the correct match?

Sun-$T_1$, tungsten filament-$T_2$, welding arc-$T_3$
Sun-$T_2$, tungsten filament-$T_1$, welding arc-$T_3$
Sun-$T_3$, tungsten filament-$T_2$, welding arc-$T_1$
Sun-$T_1$, tungsten filament-$T_3$, welding arc-$T_2$

Solution: The Wien's displacement law is $\lambda_\text{max}T=b$. The knowledge of $\lambda_\text{max}$ or $T$ of the given sources will help in getting the answer. Typical temperature of tungsten filament in lamp is 3000 K. The surface temperature of the sun is 5800 K. The temperature of welding arc varies from 6000 K to 30000 K.

Problem from IIT JEE 2004

Three discs, $A$, $B$ and $C$ having radii 2 m, 4 m and 6 m, respectively are coated with carbon black on their outer surfaces. The wavelengths corresponding to maximum intensity are 300 nm, 400 nm and 500 nm, respectively. The power radiated by them are $Q_A$, $Q_B$ and $Q_C.$ Then,

$Q_A$ is maximum
$Q_B$ is maximum
$Q_C$ is maximum
$Q_A=Q_B=Q_C$

Solution: The temperature of a black body and the wavelength corresponding to its maximum intensity are related by the Wien's displacement law, \begin{align} \lambda_m T=b. \end{align} The power radiated by a black body at temperature $T$ having surface area $A$ and emissivity $e$ is given by the Stefan's law, \begin{align} Q=\sigma e A T^4. \end{align} For a thin disc of radius $r$ emitting from both surfaces, $A=2\pi r^2$. Eliminate $T$ from above equations and substitute for $A$ to get, \begin{align} Q=2\pi\sigma e b^4 \left( r^2/\lambda_m^4\right), \nonumber \end{align} which gives, \begin{align} Q_A:Q_B:Q_C&=\frac{r_A^2}{\lambda_{A}^4}:\frac{r_B^2}{\lambda_{B}^4}:\frac{r_C^2}{\lambda_{m}^4}\nonumber\\ &=0.049:0.0625:0.057. \nonumber \end{align}

Problem from IIT JEE 2000

The plots of intensity versus wavelength for three black bodies at temperatures $T_1$, $T_2$ and $T_3,$ respectively are as shown in figure. Their temperatures are such that,

$T_1 > T_2 > T_3$
$T_1 > T_3 > T_2$
$T_2 > T_3 > T_1$
$T_3 > T_2 > T_1$

Solution: The Wien's displacement law relates wavelength at which intensity attains maximum to the temperature of the body, $\lambda_m T=b$. In given cases, $\lambda_{m,1} < \lambda_{m,3} < \lambda_{m,2}$ and hence $T_1 > T_3 > T_2$.

Problem from IIT JEE 1998

A black body is at a temperature of 2880 K. The energy of radiation emitted by this body with wavelength between 499 nm and 500 nm is $U_1$, between 999 nm and 1000 nm is $U_2$ and between 1499 nm and 1500 nm is $U_3$. The Wien constant, $b=2.88\times{10}^{6}\;\mathrm{nm K}$. Then,

$U_1=0$
$U_3=0$
$U_1>U_2$
$U_2>U_1$

Solution: The Wien's displacement law gives, \begin{align} \lambda_m=\frac{b}{T}=\frac{2.88\times{10}^{6}}{2880}=1000\;\mathrm{nm}. \nonumber \end{align}

Thus radiated energy $E_\lambda$ attains its maximum at $\lambda_m=1000\;\mathrm{nm}$. The variation of $E_\lambda$ with $\lambda$ is shown in figure. The area under the curve for given wavelength range gives radiated energy in that wavelength range i.e., $U_\lambda=E_\lambda\Delta\lambda$. The figure clearly shows that $U_1 < U_3 < U_2$.

Problem from IIT JEE 1997

The intensity of radiation emitted by the sun has its maximum value at a wavelength of 510 nm and that emitted by the north star has the maximum value at 350 nm. If these stars behaves like black bodies, then the ratio of the surface temperature of the sun and the north star is,

$1.46$
$0.69$
$1.21$
$0.83$

Solution: The Wien's displacement law relates wavelength at which intensity attains maximum to the temperature of the body, $\lambda_m T=b$. Thus, \begin{align} \frac{T_\text{sun}}{T_\text{star}}=\frac{\lambda_\text{m,star}}{\lambda_\text{m,sun}}=\frac{350}{510}=0.69. \nonumber \end{align}

Questions on Wien's Displacement Law

Question 1: Which of the following is the correct expression for Wien’s displacement constant? (Here, h is Planck’s constant, c is the speed of light and k is Boltzmann’s constant)

Question 2: The blackbody spectrum of the tungsten bulb filament is shown in the figure. Which of the following statement is correct?