Focal Length of a Concave Mirror and a Convex Lens using U-V Method
Contents
1 Introduction
2 IIT JEE Solved Problems
3 Experiment Details
4 Exercise Problems
5 Do it Yourself
6 More…
1 Introduction
The sign conventions are important in geometrical optics. All distances are measured from the pole. Distances measured in the direction of the incident ray are positive and the distances measured in the direction opposite to that of the incident rays are negative. Distances measured above the principal axis are positive and that measured below the principal axis are negative.
The object distance u, image distance v and the focal length f for a spherical mirror are related by the mirror formula
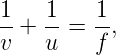 |
and for the spherical lens are related by the lens formula
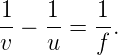 |
The u-v method to find focal length of a given concave mirror or convex lens consists of following steps
- For an appropriate object distance u, find the image distance v. Measure u and v.
- Repeat above step at few more object distances. Get the focal length
from all measurements by (a) taking average of calculated f or
(b) from u versus v graph or (c) from
 versus
versus  graph.
graph.
1.1 Concave Mirror
Look at the ray diagram shown in the figure. The distances are measured from the pole P. The incident ray (from the object to the mirror) is from the left to the right. Thus, u, v and f are all negative (by sign convention).
The
- The graph is hyperbola with asymptotes at
u =f andv =f i.e., for the object placed at F the image is formed at infinity and for the object placed at infinity the image is formed at F. - The values of
u andv are equal at point C, which corresponds tou =v = 2f . This point is the intersection ofu - v curve and the straight linev =u . This represents centre of curvature of the mirror.
The 1
1.2 Convex Lens
Look at the ray diagram shown in the figure. Note that
The
- The graph is hyperbola with asymptotes at
u =- f andv =f i.e., for the object placed at F the image is formed at infinity and for the object at infinity the image is formed at F. - At the point C, the values of
u andv are equal in magnitude but opposite in sign i.e.,v =- u = 2f . This point is the intersection ofu - v curve and the straight linev =- u . If an object is placed at a distance 2f from the pole then its image is formed at a distance 2f from the pole (on the other side).
The 1
2 IIT JEE Solved Problems
x < f f < x < 2f x = 2f x > 2f
In general, the concept of parallax is memorized by the students without
understanding it. Let
In given case, when eye is shifted towards left, the image appears to
the right of the object pin. Thus, image lies between the eye and the
object pin. Hence, the object is near to the pole
- (42
, 56) - (48
, 48) - (66
, 33) - (78
, 39)
- 5
± 0. 1 - 5
± 0. 05 - 0
. 5± 0. 1 - 0
. 5± 0. 05
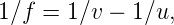 |
to get
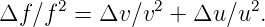 |
Substitute
- a concave mirror of suitable focal length.
- a convex mirror of suitable focal length.
- a convex lens of focal length less than 0
. 25m. - a concave lens of suitable focal length.
Consider the case when we place a concave mirror (see figure). Let
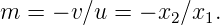 |
For a diminished image,
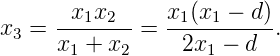 |
Thus, if we take
Now, consider the case when we place a convex lens. Let
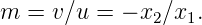 |
For diminished image,
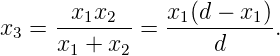 |
The condition
- Convex lens
- Concave lens
- Convex mirror
- Concave mirror
- half of the image will disappear.
- complete image will be formed.
- intensity of the image will increase.
- intensity of the image will decrease.
3 Experiment Details
3.1 Procedure
The procedure to find focal length of a convex lens by
- Fix the given concave mirror on the stand. Arrange the screen on
the table so that the image of the distant object is obtained on it.
Measure the distance between mirror and screen using a metre scale.
This distance is the approximate focal length (
f ) of the mirror. - Set the values of
u ranging from 1. 5f to 2. 5f . Divide the range into a number of equal steps. - Place the mirror in front of an illuminated object. Now, fix the mirror
at the distance
u (which is obtained as 1. 5f ). - Place the screen on the table facing the mirror in such a way that the reflected image lies on the screen. Keeping the distance between object and mirror fixed, adjust the position of screen in order to get the clear image of the object. Remove the parallax to get accurate position of the image.
- Measure the distance between mirror and object, as well as mirror and
screen. Take these values as
u andv respectively. Calculate the focal length of the given concave mirror by using the relation,f =uv∕ (u +v ). - Repeat the experiment for different values of
u (up to 2. 5f ) and in each time, measurev and record it in the tabular column. Calculate the focal length (f ) of the concave mirror each time. - Calculate the mean of all focal lengths to get the correct focal length of the given concave mirror.
- The focal length of the mirror can also be measured graphically by
plotting graphs between
u andv , and 1∕u and 1∕v .
3.2 Precautions
Some of the precautions and sources of errors are given below
- The principal axis of the mirror should be horizontal and parallel to central line of the optical bench.
- The object should be vertical.
- Index correction for
u andv should be applied.
3.3 Data Table
The data should be recorded in the tabular format. One possible format is given below:
| S.No. | | | 1 | 1 | f |
| (cm) | (cm) | (cm | (cm | (cm) | |
4 Exercise Problems
d∕ (m 1 - m 2 )d∕ (m 1 +m 2 )dm 1 ∕m 2 dm 2 ∕m 1
md ∕ (m + 1)2 md ∕ (m + 1)md ∕ (m - 1)2 md ∕ (m - 1)
- (
x +y )∕ 2 x - y 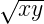
x +y
- 36 cm
- 72 cm
- 18 cm
- 9 cm
- 4 cm
- (
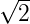 + 1) cm
+ 1) cm
- 2
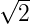 cm
cm
- (
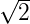 + 2) cm
+ 2) cm
- 20 cm
- 40 cm
- 30 cm
- 60 cm
x = +20 cmx =- 30 cmx =- 10 cmx = 0 cm
d d∕ 2d∕ 3d∕ 4
- virtual image is always larger in size
- real image is always smaller in size
- real image is always larger in size
- real image may be larger or smaller in size
- 40.5 cm
- -40 cm
- -45 cm
- 40 cm
u =- 10, f = 20u =- 20, f =- 30u =- 45, f =- 10u =- 60, f = 30
- must be less than 10 cm
- must be greater than 20 cm
- must not be be greater than 20 cm
- must not be less than 10 cm
- The mirror equation is one which connects
u ,v , andf . - Real inverted image with same size is obtained if the object is placed on the centre of curvature of a concave mirror.
- The image formed in concave mirror is always real.
- Concave mirrors have reflecting inner surface.
5 Do it Yourself
We believe in experiment based learning. You can do many low cost experiments at home. Some of them are given below:
5.1 Focal Length of a Concave Mirror
The material required are a concave mirror, V-stand, screen of stiff paper, screen-stand, candle, matchbox, and a scale.
- Firstly, find the approximate focal length (
f ) of a concave mirror. You can do this by focusing a distant object like sun. Fix mirror vertically on a V-stand. Draw a long straight line on a table and place the mirror stand on it. The pole of the mirror should be exactly above the line. - Light a candle and place it on one end of the line. The flame of the candle should be at the same height as the pole of the mirror.
- Fix the screen on its stand. The screen should be vertical. Place the screen between the candle and mirror.
- Analyse the nature of the image by moving the screen and/or mirror.
- For three different values of
u , find the value ofv . Calculatef by substituting in mirror formula.
5.2 Focal Length of the Convex Lens
The material required are a convex mirror, V-stand, screen of stiff paper, screen-stand, candle, matchbox, and a scale.
- Firstly, find the approximate focal length (
f ) of the convex lens. Then fix it vertically on a V-stand. Draw a long straight line on a table and place the lens in the middle. The pole of the lens should be exactly above the line. - Light a candle and place it on one end of the line. The flame of the candle should be at the same height as the pole of the lens.
- Fix the screen on its stand. The screen should be vertical. Place the screen on other side of the lens.
- Analyse the nature of the image by moving the screen and/or lens.
- For three different values of
u , find the value ofv . Calculatef by substituting in the lens formula.
6 More…
There are more methods to find focal length of the convex lens [7].
6.1 Plane Mirror Method
In the plane mirror method, the lens is placed on the mirror and the object is moved until object and image coincide. This point is the principal focus, since light from it will emerge parallel from the lens and so be reflected back along its original path when it strikes the mirror. The object can be either a pin or a point source. Following IIT JEE problem is based on this method:
- virtual and at a distance of 16cm from the mirror.
- real and at a distance of 16cm from the mirror.
- virtual and at a distance of 20cm from the mirror.
- real and at a distance of 20cm from the mirror.
6.2 Displacement Method or Two Position Method
An illuminated object is set up in front of a lens and a focused image is formed on a screen. For a given separation of the object and screen it will be found that there are two positions where a clearly focused image can be formed. By the principle or reversibility these must be symmetrical between object position O and the image position I.
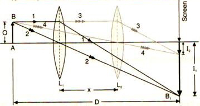
If
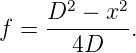 |
The readers are advised to prove this result. Also, the method works only when
6.3 The Minimum Distance Method
This method is based on the fact that there is a minimum separation for object
and image for a given lens. This can be shown if
References
[1] Focal length of a concave mirror by u-v method.
[2] Focal length of
a convex lens by u-v method.
[3] Focal length of
concave mirror by u-v method.
[4] Focal length of concave mirror by u-v method.
[5] Focal length of the concave mirror.
[6] Focal length of the convex lens.
[7] The measurement of
the focal length of a lens.
[8] NCERT book to find the focal length of a convex lens.
[9] HC Verma.

JEE PYQ+ Physics Books
Solve past year JEE questions with detailed explanations.