Elastic and Inelastic Collisions
The linear momentum of the system is conserved in a collision.
The coefficient of restitution is defined as the ratio of the magnitudes of the initial and final relative velocities i.e., \begin{align} e&=\frac{\text{velocity of separation}}{\text{velocity of approach}}\\ &=\frac{-(v_1^\prime-v_2^\prime)}{v_1-v_2} \end{align}
In an elastic collision, coefficient of restitution is 1 and change in kinetic energy is zero.
Elastic Collision in One Dimension
The conservation of linear momentum gives \begin{align} m_1 v_1 +m_2 v_2=m_1 v_1^\prime +m_2 v_2^\prime \end{align} The change in kinetic energy is zero i.e., \begin{align} \frac{1}{2}m_1 v_1^2 + \frac{1}{2} m_2 v_2^2=\frac{1}{2}m_1 {v_1^\prime}^2 +\frac{1}{2}m_2 {v_2^\prime}^2 \end{align} These two equations gives \begin{align} v_1-v_2=-(v_1^\prime - v_2^\prime) \end{align} The velocities of two particles after the collision are given by \begin{align} v_1^\prime & =\frac{m_1-m_2}{m_1+m_2}v_1+\frac{2m_2}{m_1+m_2}v_2 \\ v_2^\prime & =\frac{2m_1}{m_1+m_2}v_1-\frac{m_1-m_2}{m_1+m_2}v_2 \end{align}
If $m_1 \gg m_2$ then $v_1^\prime \approx v_1$ and $v_2^\prime = 2v_1-v_2$. The heavier body continues to move with almost the same velocity. If the lighter body were kept at rest ($v_2 = 0$) then it fly away with a velocity double the velocity of the heavier body ($v_2^\prime = 2v_1$). This happens when a speeding heavy truck hits a stationary car.
If $m_2 \gg m_1 $ then $v_1^\prime \approx -v_1+2 v_2$ and $v_2^\prime = v_2$. The heavier body continues to move with almost the same velocity. If heavier body is at rest ($v_2 = 0$) then $v_1^\prime = -v_1$, the lighter body bounces back with the same speed. This happens when a ball collides elastically with a fixed wall.
If masses of the colliding bodies are same ($m_1 = m_2$) then $v_1^\prime=v_2$ and $v_2^\prime = v_1$. The two balls exchange their velocities.
In centre of mass frame, the particles just reverses their velocities.
Completely Inelastic Collision in One Dimension
In a completely inelastic collision, two particles stick together after the collision. The coefficient of restitution is zero because velocity of separation is zero. Apply conservation of linear momentum to get the velocity of two particles after the collision \begin{align} V=\frac{m_1v_1+m_2 v_2}{m_1+m_2} \end{align}
The loss in kinetic energy in a completely inelastic collision is given by \begin{align} \Delta K&=\frac{1}{2}\frac{m_1m_2}{m_1+m_2}(v_1-v_2)^2 \end{align}
Elastic Collision in Two Dimensions
In a elastic collision in two dimensions- Apply conservation of linear momentum in two perpendicular directions.
- The change in kinetic energy is zero.
- The equal mass particles emerge from a two-dimensional elastic collision at right angles.
Solved Problems from IIT JEE
Problem from IIT JEE 2009
Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These have masses $m$, $2m$ and $m$, respectively. The object A moves towards B with a speed 9 m/s and makes an elastic collision with it. Thereafter, B makes completely inelastic collision with C. All motions occur on the same straight line. Find the final speed (in m/s) of the object C.
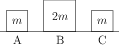
Solution: Let $v_A$ and $v_B$ be the velocities of A and B after an elastic collision. The conservation of linear momentum gives, \begin{align} \label{rfa:eqn:1} m\times 9+0=mv_A+2mv_B. \end{align} The conservation of energy gives, \begin{align} \label{rfa:eqn:2} \tfrac{1}{2}m\times 9^2+0=\tfrac{1}{2}mv_A^2+\tfrac{1}{2}\,(2m)v_B^2. \end{align} Solve above equations to get $v_B={6}\;\mathrm{m/s}$. The collision between B and C is completely inelastic i.e., after the collision both particles coalesce and move with a common speed, say $v_C$. The conservation of linear momentum gives, \begin{align} \label{rfa:eqn:3} (2m)\times 6+0=(2m+m)v_C. \end{align} Solve to get $v_C=4\;\mathrm{m/s}$.
Problem from IIT JEE 2007
Statement 1: In an elastic collision between two bodies, the relative speed of the bodies after collision is equal to the relative speed before the collision.
Statement 2: In an elastic collision, the linear momentum of the system is conserved.
- Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
- Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
- Statement 1 is true, statement 2 is false.
- Statement 1 is false, statement 2 is true.
Solution: Let $v_s$ be the velocity of separation and $v_a$ be the velocity of approach. The $v_s$ and $v_a$ are related by, $v_s=e v_a$, where $e$ is the coefficient of restitution. The energy conservation in elastic collision gives $e=1$.
Related
- Kinetic and Potential Energy
- Work-Energy Theorem
- Conservation of Mechanical Energy
- Centre of Mass and its Motion
